题目内容
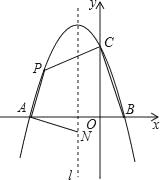
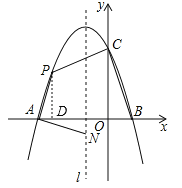
【题目】如图,抛物线y=ax2+bx+c与x轴交于点A和点B(1,0),与y轴交于点C(0,3),其对称轴l为x=﹣1.
(1)求抛物线的解析式并写出其顶点坐标;
(2)若动点P在第二象限内的抛物线上,动点N在对称轴l上.
①当PA⊥NA,且PA=NA时,求此时点P的坐标;
②当四边形PABC的面积最大时,求四边形PABC面积的最大值及此时点P的坐标.
【答案】(1)y=﹣(x+1)2+4,顶点坐标为(﹣1,4);(2)①点P(﹣![]() ﹣1,2);②P(﹣
﹣1,2);②P(﹣![]() ,
, ![]() )
)
【解析】试题分析:(1)将B、C的坐标代入已知的抛物线的解析式,由对称轴为![]() 即可得到抛物线的解析式;
即可得到抛物线的解析式;
(2)①首先求得抛物线与x轴的交点坐标,然后根据已知条件得到PD=OA,从而得到方程求得x的值即可求得点P的坐标;
②![]() ,表示出来得到二次函数,求得最值即可.
,表示出来得到二次函数,求得最值即可.
试题解析:(1)∵抛物线![]() 与x轴交于点A和点B(1,0),与y轴交于点C(0,3),其对称轴l为
与x轴交于点A和点B(1,0),与y轴交于点C(0,3),其对称轴l为![]() ,∴
,∴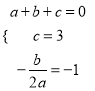 ,解得:
,解得: 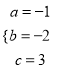 ,∴二次函数的解析式为
,∴二次函数的解析式为![]() =
=![]() ,∴顶点坐标为(﹣1,4);
,∴顶点坐标为(﹣1,4);
(2)令![]() ,解得
,解得![]() 或
或![]() ,∴点A(﹣3,0),B(1,0),作PD⊥x轴于点D,∵点P在
,∴点A(﹣3,0),B(1,0),作PD⊥x轴于点D,∵点P在![]() 上,∴设点P(x,
上,∴设点P(x, ![]() ),
),
①∵PA⊥NA,且PA=NA,∴△PAD≌△AND,∴OA=PD,即![]() ,解得x=
,解得x=![]() (舍去)或x=
(舍去)或x=![]() ,∴点P(
,∴点P(![]() ,2);
,2);
②设P(x,y),则![]() ,∵
,∵![]()
=![]() OBOC+
OBOC+![]() ADPD+
ADPD+![]() (PD+OC)OD=
(PD+OC)OD=![]() =
= ![]()
=![]() =
=![]() =
=![]() ,
,
∴当x=![]() 时,
时, ![]() =
=![]() ,当x=
,当x=![]() 时,
时, ![]() =
=![]() ,此时P(
,此时P(![]() ,
, ![]() ).
).

练习册系列答案
 小学课时特训系列答案
小学课时特训系列答案
相关题目