题目内容
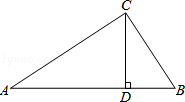
【题目】如图所示,在四边形ABCD中,AD∥BC,AB=AD,∠BAD的平分线AE交BC于点E,连接DE.
(1)求证:四边形ABED是菱形;
(2)若∠DEC=60°,CE=2DE=4cm,求CD的长.

【答案】(1)见解析;(2)CD=2![]()
【解析】整体分析:
(1)用SAS证明△BAE≌△DAE,判断四边形ABED的四边都相等;(2)过点D作DF∥AE交BC于点F,判断四边形AEFD是平行四边形,△DEF是等边三角形,证明△EDC是直角三角形,用勾股定理求解.
(1)证明:如图,∵AE平分∠BAD,∴∠1=∠2,
∵AB=AD,AE=AE,
∴△BAE≌△DAE,
∴BE=DE,
∵AD∥BC,∴∠2=∠3=∠1,∴AB=BE,
∴AB=BE=DE=AD,
∴四边形ABED是菱形.
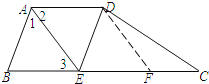
(2)解:如图,过点D作DF∥AE交BC于点F,则四边形AEFD是平行四边形,
∴DF=AE,AD=EF,
∵四边形ABED是菱形,
∴AB=BE=DE=AD,
∴DE=EF,
又∵∠ABC=60°,
∴∠DEF=60°,
∴△DEF是等边三角形,
∵CE=2DE,∴EF=FC,
∴DF=EF=FC,
∴△CDE是直角三角形.
由勾股定理求得CD=2![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目