题目内容
【题目】如图,ABCD是正方形,G是BC上(除端点外)的任意一点,DE⊥AG于点E,BF∥DE,交AG于点F.下列结论不一定成立的是【 】
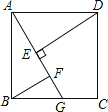
A.△AED≌△BFA B.DE﹣BF=EF C.△BGF∽△DAE D.DE﹣BG=FG
【答案】D
【解析】∵四边形ABCD是正方形,∴AB=AD,AD∥BC,
∵DE⊥AG,BF∥DE,∴BF⊥AG。∴∠AED=∠DEF=∠BFE=90°。
∵∠BAF+∠DAE=90°,∠DAE+∠ADE=90°,∴∠BAF=∠ADE。
∴△AED≌△BFA(AAS)。故结论A正确。
∴DE=AF,AE=BF,∴DE﹣BF=AF﹣AE=EF。故结论B正确。
∵AD∥BC,∴∠DAE=∠BGF。
∵DE⊥AG,BF⊥AG,∴∠AED=∠GFB=90°。∴△BGF∽△DAE。故结论C正确。
由△ABF∽△AGB得![]() ,即
,即![]() 。
。
由勾股定理得,![]() 。
。
∴![]()
![]() 。
。
∵![]() (只有当∠BAG=300时才相等,由于G是的任意一点,∠BAG=300不一定),
(只有当∠BAG=300时才相等,由于G是的任意一点,∠BAG=300不一定),
∴![]() 不一定等于
不一定等于![]() ,即DE﹣BG=FG不一定成立。故结论D不正确。故选D。
,即DE﹣BG=FG不一定成立。故结论D不正确。故选D。

练习册系列答案
 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案
相关题目