题目内容
【题目】如图,已知一次函数y=kx﹣4k+5的图象与反比例函数y= ![]() (x>0)的图象相交于点A(p,q).当一次函数y的值随x的值增大而增大时,p的取值范围是 .
(x>0)的图象相交于点A(p,q).当一次函数y的值随x的值增大而增大时,p的取值范围是 . 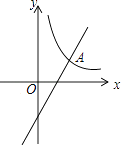
【答案】![]() <p<4
<p<4
【解析】解:一次函数y=kx﹣4k+5中,令x=4,则y=5, 故一次函数y=kx﹣4k+5的图象经过点(4,5),
如图所示,过点(4,5)分别作y轴与x轴的垂线,分别交反比例函数图象于B点和C点,
把y=5代入y= ![]() ,得x=
,得x= ![]() ;
;
把x=4代入y= ![]() ,得y=
,得y= ![]() ,
,
所以B点坐标为( ![]() ,5),C点坐标为(4,
,5),C点坐标为(4, ![]() ),
),
因为一次函数y的值随x的值增大而增大,
所以点A(p,q)只能在B点与C点之间的曲线上,
所以p的取值范围是 ![]() <p<4.
<p<4.
所以答案是: ![]() <p<4.
<p<4.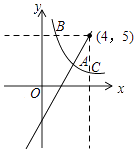

练习册系列答案
相关题目
【题目】如图所示,在四边形ABCD中,AD∥BC,AB=AD,∠BAD的平分线AE交BC于点E,连接DE.
(1)求证:四边形ABED是菱形;
(2)若∠DEC=60°,CE=2DE=4cm,求CD的长.

【题目】如图所示,若将类似于a、b、c、d四个图的图形称做平面图,则其顶点数、边数与区域数之间存在某种关系.观察图b和表中对应的数值,探究计数的方法并作答.

(1)数一数每个图中各有多少个顶点、多少条边,这些边围出多少个区域并填表:
平面图 | a | b | c | d |
顶点数(S) | 7 | |||
边数(M) | 9 | |||
区域数(N) | 3 |
(2)根据表中数值,写出平面图的顶点数、边数、区域数之间的一种关系为 ;
(3)如果一个平面图有20个顶点和11个区域,那么利用(2)中得出的关系可知这个平面图有 条边.