题目内容
【题目】解不等式组 
并写出它的所有非负整数解．
【答案】解：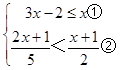 
， 解不等式①得x≤1，
解不等式②得x＞﹣3，
∴不等式组的解集是：﹣3＜x≤1．
∴不等式组的非负整数解为0，1
【解析】先求出不等式组的解集，再求出不等式组的非负整数解即可．
【考点精析】掌握一元一次不等式组的解法和一元一次不等式组的整数解是解答本题的根本，需要知道解法：①分别求出这个不等式组中各个不等式的解集；②利用数轴表示出各个不等式的解集；③找出公共部分；④用不等式表示出这个不等式组的解集．如果这些不等式的解集的没有公共部分，则这个不等式组无解 ( 此时也称这个不等式组的解集为空集 )；使不等式组中的每个不等式都成立的未知数的值叫不等式组的解，一个不等式组的所有的解组成的集合，叫这个不等式组的解集(简称不等式组的解)．
【题目】如图所示，在四边形ABCD中，AD∥BC，AB=AD，∠BAD的平分线AE交BC于点E，连接DE．
（1）求证：四边形ABED是菱形；
（2）若∠DEC=60°，CE=2DE=4cm，求CD的长．
【题目】某公司需招聘一名员工，对应聘者甲、乙、丙从笔试、面试、体能三个方面进行量化考核．甲、乙、丙各项得分如下表：
笔 试 | 面 试 | 体 能 | |
甲 | 85 | 80 | 75 |
乙 | 80 | 90 | 73 |
丙 | 83 | 79 | 90 |
（1）根据三项得分的平均分，从高到低确定三名应聘者的排名顺序．
（2）该公司规定：笔试，面试、体能得分分别不得低于80分，80分，70分，并按60%，30%，10%的比例计入总分（不计其他因素条件），请你说明谁将被录用．
【题目】如图所示，若将类似于a、b、c、d四个图的图形称做平面图，则其顶点数、边数与区域数之间存在某种关系．观察图b和表中对应的数值，探究计数的方法并作答．
（1）数一数每个图中各有多少个顶点、多少条边，这些边围出多少个区域并填表：
平面图 | a | b | c | d |
顶点数(S) | 7 | |||
边数(M) | 9 | |||
区域数(N) | 3 |
（2）根据表中数值，写出平面图的顶点数、边数、区域数之间的一种关系为 ；
（3）如果一个平面图有20个顶点和11个区域，那么利用（2）中得出的关系可知这个平面图有 条边．