题目内容
3.一个等腰三角形的三边长分别为x,2x-3,4x-6,求这个三角形的周长.分析 根据等腰三角形的性质可分x=2x-3、x=4x-6和2x-3=4x-6三种情况考虑,求出三种情况下三边长度,利用三角形的三边关系确定三角形是否存在,若存在再利用三角形的周长公式求出周长即可.
解答 解:①x=2x-3,则x=3,
∴4x-6=6,
∵3+3=6,
∴3、3、6不能构成三角形;
②x=4x-6,则x=2,
∴2x-3=1,
∵1、2、2任意两边之和大于第三边,
∴这个三角形的周长为1+2+2=5;
③2x-3=4x-6,则x=$\frac{3}{2}$,
∴2x-3=0,
∴此三角形不存在.
综上可知:这个三角形的周长为5.
点评 本题考查了等腰三角形的性质以及三角形三边关系,分x=2x-3、x=4x-6和2x-3=4x-6三种情况来考虑是解题的关键.

练习册系列答案
相关题目
8.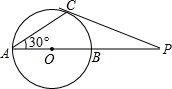 已知⊙O的直径AB与弦AC的夹角为30°,过C点的切线PC与AB延长线交P,⊙O的半径为5,则BP的长为( )
已知⊙O的直径AB与弦AC的夹角为30°,过C点的切线PC与AB延长线交P,⊙O的半径为5,则BP的长为( )
 已知⊙O的直径AB与弦AC的夹角为30°,过C点的切线PC与AB延长线交P,⊙O的半径为5,则BP的长为( )
已知⊙O的直径AB与弦AC的夹角为30°,过C点的切线PC与AB延长线交P,⊙O的半径为5,则BP的长为( )| A. | $\frac{{5\sqrt{3}}}{3}$ | B. | $\frac{{5\sqrt{3}}}{6}$ | C. | 10 | D. | 5 |
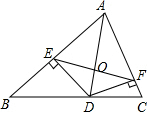 如图,AD为△ABC的角平分线,DE⊥AB于点E,DF⊥AC于点F,EF交AD于点O,求证:OF=OE.
如图,AD为△ABC的角平分线,DE⊥AB于点E,DF⊥AC于点F,EF交AD于点O,求证:OF=OE.
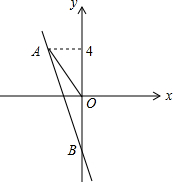 如图,点A(a,4)在一次函数y=-3x-5的图象上,图象与y轴的交点为B,那么△AOB的面积为7.5.
如图,点A(a,4)在一次函数y=-3x-5的图象上,图象与y轴的交点为B,那么△AOB的面积为7.5.
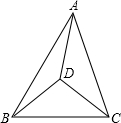 如图,△ABC内有一点D,且DA=DB=DC,若∠DAB=20°,则∠ACB的度数为70度.
如图,△ABC内有一点D,且DA=DB=DC,若∠DAB=20°,则∠ACB的度数为70度.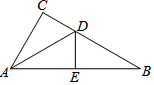 如图,在Rt△ABC中,∠C=90°,∠B=30°,AD平分∠CAB交BC于D,DE⊥AB于E.若DE=1cm,则BC=( )cm.
如图,在Rt△ABC中,∠C=90°,∠B=30°,AD平分∠CAB交BC于D,DE⊥AB于E.若DE=1cm,则BC=( )cm.