题目内容
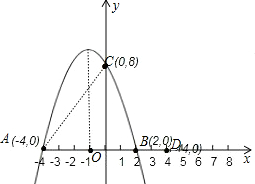
已知抛物线y=ax2+bx+c的图象交x轴于点A(x0,0)和点B(2,0),与y轴的正半轴交于点C,其对称轴是直线x=-1,tan∠BAC=2,点A关于y轴的对称点为点D.
(1)确定A、C、D三点的坐标;
(2)求过B、C、D三点的抛物线的解析式;
(3)若过点(0,3)且平行于x轴的直线与(2)小题中所求抛物线交于M、N两点,以MN为一边,抛物线上任意一点P(x,y)为顶点作平行四边形,若平行四边形的面积为S,写出S关于P点纵坐标y的函数解析式;
(4)当
<x<4时,(3)小题中平行四边形的面积是否有最大值?若有,请求出;若无,请说明理由.
(1)确定A、C、D三点的坐标;
(2)求过B、C、D三点的抛物线的解析式;
(3)若过点(0,3)且平行于x轴的直线与(2)小题中所求抛物线交于M、N两点,以MN为一边,抛物线上任意一点P(x,y)为顶点作平行四边形,若平行四边形的面积为S,写出S关于P点纵坐标y的函数解析式;
(4)当
| 1 |
| 2 |
(1)∵点A与点B关于直线x=-1对称,点B的坐标是(2,0)
∴点A的横坐标是
=-1,x0=-4,
故点A的坐标是(-4,0)
∵tan∠BAC=2即
=2,可得OC=8
∴C(0,8)
∵点A关于y轴的对称点为D
∴点D的坐标是(4,0);
(2)设过三点的抛物线解析式为y=a(x-2)(x-4),
代入点C(0,8),解得a=1.
∴抛物线的解析式是y=x2-6x+8;
(3)∵抛物线y=x2-6x+8与过点(0,3)平行于x轴的直线相交于M点和N点
∴M(1,3),N(5,3),
而抛物线的顶点为(3,-1),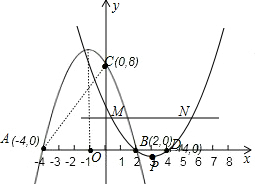
当y>3时,
S=4(y-3)=4y-12,
当-1≤y<3时,
S=4(3-y)=-4y+12;
(4)以MN为一边,P(x,y)为顶点,且当<x<4的平行四边形面积最大,只要点P到MN的距离h最大
∴当x=3,y=-1时,h=4,
S=4h=4×4=16,
∴满足条件的平行四边形面积有最大值16.
∴点A的横坐标是
| x0+2 |
| 2 |
故点A的坐标是(-4,0)
∵tan∠BAC=2即
| OC |
| |OA| |
∴C(0,8)
∵点A关于y轴的对称点为D
∴点D的坐标是(4,0);
(2)设过三点的抛物线解析式为y=a(x-2)(x-4),
代入点C(0,8),解得a=1.
∴抛物线的解析式是y=x2-6x+8;
(3)∵抛物线y=x2-6x+8与过点(0,3)平行于x轴的直线相交于M点和N点
∴M(1,3),N(5,3),
而抛物线的顶点为(3,-1),

当y>3时,
S=4(y-3)=4y-12,
当-1≤y<3时,
S=4(3-y)=-4y+12;
(4)以MN为一边,P(x,y)为顶点,且当<x<4的平行四边形面积最大,只要点P到MN的距离h最大
∴当x=3,y=-1时,h=4,
S=4h=4×4=16,
∴满足条件的平行四边形面积有最大值16.


练习册系列答案
相关题目
 的⊙M上的两点,且tan∠AOB=
的⊙M上的两点,且tan∠AOB=

 边AB的长为x(单位:米),矩形ABCD的面积为S(单位:平方米).
边AB的长为x(单位:米),矩形ABCD的面积为S(单位:平方米).
 ),⊙M与y轴的正半轴交于点C.
),⊙M与y轴的正半轴交于点C.