题目内容
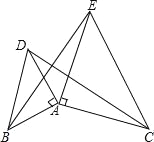
【题目】如图,已知△ABC的面积为16,BC=8.现将△ABC沿直线BC向右平移a个单位到△DEF的位置.
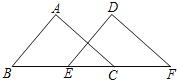
(1)当△ABC所扫过的面积为32时,求a的值;
(2)连接AE、AD,当AB=5,a=5时,试判断△ADE的形状,并说明理由.
【答案】(1)a=4;(2)△ADE为等腰三角形.
【解析】
(1)作AH⊥BC于H,根据△ABC的面积为16,BC=8,可先求出AH的长,由△ABC所扫过的面积为32,求出a的值;(2)根据平移的性质可知AB=DE=5,又AD=5,即可推出△ADE为等腰三角形.
(1)△ABC所扫过面积即梯形ABFD的面积,作AH⊥BC于H,
∵S△ABC=16,
∴![]() BCAH=16,
BCAH=16,
∵BC=8,
∴AH=4,
∴S四边形ABFD=![]() ×(AD+BF)×AH
×(AD+BF)×AH
=![]() (a+a+8)×4=32,
(a+a+8)×4=32,
解得:a=4.
(2)△ADE为等腰三角形,理由如下:
根据平移的性质可知DE=AB=5,
又∵AD=a=5,
∴△ADE为等腰三角形.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目