题目内容
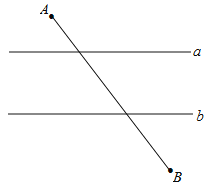
【题目】如图，已知直线a∥b，且a与b之间的距离为4，点A到直线a的距离为2，点B到直线b的距离为3，AB
．试在直线a上找一点M，在直线b上找一点N，满足MN⊥a且AM+MN+NB的长度和最短，则此时AM+NB＝（ ）
A. 6 B. 8 C. 10 D. 12
【答案】B
【解析】
MN表示直线a与直线b之间的距离，是定值，只要满足AM+NB的值最小即可．过A作直线a的垂线，并在此垂线上取点A′，使得AA′＝MN，连接A'B，则A'B与直线b的交点即为N，过N作MN⊥a于点M．则A'B为所求，利用勾股定理可求得其值．
过A作直线a的垂线，并在此垂线上取点A′，使得AA′＝4，连接A′B，与直线b交于点N，过N作直线a的垂线，交直线a于点M，连接AM，过点B作BE⊥AA′，交射线AA′于点E，如图，∵AA′⊥a，MN⊥a，∴AA′∥MN．
又∵AA′＝MN＝4，∴四边形AA′NM是平行四边形，∴AM＝A′N．
由于AM+MN+NB要最小，且MN固定为4，所以AM+NB最小．
由两点之间线段最短，可知AM+NB的最小值为A′B．
∵AE＝2+3+4＝9，AB
，∴BE
．
∵A′E＝AE﹣AA′＝9﹣4＝5，∴A′B
8．
所以AM+NB的最小值为8．
故选B．
练习册系列答案
相关题目
