题目内容
【题目】已知AB为⊙O的直径,CD为⊙O的弦,CD∥AB,过点B的切线与射线AD交于点M,连接AC,BD.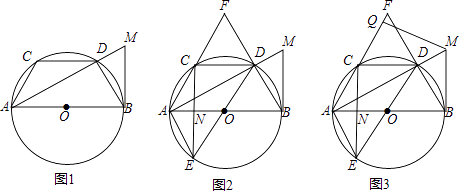
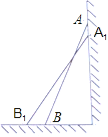
(1)如图l,求证:AC=BD;
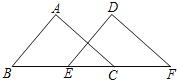
(2)如图2,延长AC、BD交于点F,作直径DE,连接AE、CE,CE与AB交于点N,求证:∠AFB=2∠AEN;
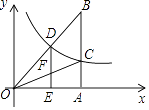
(3)如图3,在(2)的条件下,过点M作MQ⊥AF于点Q,若MQ:QC=3:2,NE=2,求QF的长.
【答案】
(1)证明:连接OC,OD,
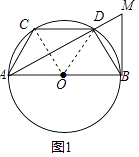
∵CD∥AB,
∴∠DAB=∠ADC,
∵∠DOB=2∠DAB,∠COA=2∠CDA,
∴∠COA=∠DOB,
∴AC=BD;
(2)连接OC,
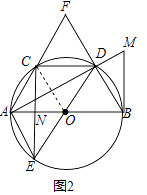
∵∠COA=∠DOB,OA=OB=OC=OD,
∴∠CAB=∠DBA,
∴△FBA是等腰三角形,
∵DE是⊙O的直径,
∴∠ECD=90°,
∵CD∥AB,
∴∠ANC=90°,
∴AB⊥CE,
∴AC=AE,
∴∠CAN=∠EAN=∠ABF,∠ACE=∠AEN,
∵∠FAB+∠FBA+∠F=180°,∠CAE+∠AEC+∠ACE=180°,
∴∠F=∠ACE+∠AEC,
∴∠AFB=2∠AEN;
(3)解:连接BC交AD于P,
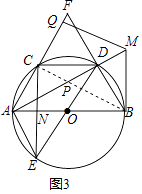
∵AC=BD,
∴ ![]() =
= ![]() ,
,
∴∠PAB=∠PBA,
∴PA=PB,∠PBM=∠PMB,
∴PB=PM,
∴P为AM的中点,
∵MQ⊥AF,BC⊥AF,
∴BC∥MQ,
∴ ![]() =
= ![]() ,
,
∴AC=CQ,
∵ ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() ,
,
∴tan∠MAQ= ![]() ,
,
∴tan∠F= ![]() ,
,
设DF=3k,AD=4k,由勾股定理得,AF=5k=BF,
∴BD=2k,
∴tan∠ABD=2,
∴DE为直径,
∴∠EAD=90=∠BDM,
∴AE∥BD,
∴∠EAN=∠ABD,
∴tan∠EAN=2,
∵NE=2,
∴AN=1,CN=2,
∴BN=4,AE=BD= ![]() ,
,
∴DF= ![]() ,AC=BD=
,AC=BD= ![]() =CQ,
=CQ,
∴QF= ![]()
【解析】(1)由平行线的内错角相等性质、圆周角定理可推出AC=BD;(2)由于∠AEN是圆周角,因此2∠AEN可转化为圆心角∠COA,问题转化为证∠COA=∠AFB,两个角都是等腰三角形的顶角,转化为证底角相等,即∠CAN=∠EAN=∠ABF,由垂径定理推论易证出结论;(3)利用圆周角定理的推论可推出tan∠MAQ= ![]() ,进而推出tan∠F=
,进而推出tan∠F= ![]() ,设出参数,求出AC,进而求出AQ,用AF减去AQ可求出QF
,设出参数,求出AC,进而求出AQ,用AF减去AQ可求出QF

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案