题目内容
如图，矩形ABCD中，AB=4，BC=5，AF平分∠DAE，EF⊥AE，则CF等于（ ）
| A．1 | B．2 | C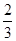． | D． |
D
∵四边形ABCD是矩形，∴AD=BC=5，∠D=∠B=∠C=90°，
∵AF平分∠DAE，EF⊥AE，∴DF=EF，
由勾股定理得：AE=AD=5，在△ABE中由勾股定理得：BE=
=3，
∴EC=5﹣3=2，∵∠BAE+∠AEB=90°，∠AEB+∠FEC=90°，∴∠BAE=∠FEC，∴△ABE∽△ECF，
∴
=
，∴
=
，∴CF=
．故选D
∵AF平分∠DAE，EF⊥AE，∴DF=EF，
由勾股定理得：AE=AD=5，在△ABE中由勾股定理得：BE=
=3，∴EC=5﹣3=2，∵∠BAE+∠AEB=90°，∠AEB+∠FEC=90°，∴∠BAE=∠FEC，∴△ABE∽△ECF，
∴
=，∴=，∴CF=．故选D
练习册系列答案
名校课堂系列答案
相关题目
的平分线AE交BC边于点E；②以AC边上一点Ｏ为圆心，过A、E两点作圆Ｏ（尺规作图，不写作法，保留作图痕迹）；
的位置关系，并说明理由；
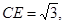求线段CE、CF与劣弧EF所围成的图形面积．（结果保留根号和Π）
，则等腰梯形的腰长是________cm．