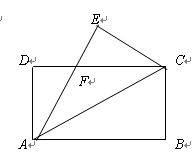
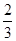题目内容
如图,在矩形ABCD中,
小题1:请完成如下操作:①作 的平分线AE交BC边于点E;②以AC边上一点O为圆心,过A、E两点作圆O(尺规作图,不写作法,保留作图痕迹);
的平分线AE交BC边于点E;②以AC边上一点O为圆心,过A、E两点作圆O(尺规作图,不写作法,保留作图痕迹);
小题2:请在(1)的基础上,完成下列问题:
①判断直线BC与圆 的位置关系,并说明理由;
的位置关系,并说明理由;
②若圆 与AC边的另一个交点为F,
与AC边的另一个交点为F,
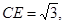 求线段CE、CF与劣弧EF所围成的图形面积.(结果保留根号和Π)
求线段CE、CF与劣弧EF所围成的图形面积.(结果保留根号和Π)

小题1:请完成如下操作:①作
 的平分线AE交BC边于点E;②以AC边上一点O为圆心,过A、E两点作圆O(尺规作图,不写作法,保留作图痕迹);
的平分线AE交BC边于点E;②以AC边上一点O为圆心,过A、E两点作圆O(尺规作图,不写作法,保留作图痕迹);小题2:请在(1)的基础上,完成下列问题:
①判断直线BC与圆
 的位置关系,并说明理由;
的位置关系,并说明理由;②若圆
 与AC边的另一个交点为F,
与AC边的另一个交点为F,
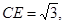 求线段CE、CF与劣弧EF所围成的图形面积.(结果保留根号和Π)
求线段CE、CF与劣弧EF所围成的图形面积.(结果保留根号和Π)
小题1:①作∠BAC的平分线AE交BC于点E; 1分

②作AE的垂直平分线交AC于点O,以O为圆心,OA为半径作圆
小题2:①判断:直线BC与圆O相切。 3分
理由:连接OE
因为:AE平分角EAB
所以:∠EAC=∠EAB
因为:OA=OE,所以:∠OEA=∠OAE
所以:∠EAB=∠OEA 所以OE//AB 5分
所以:∠OEC=∠B
因为:∠B=90度,
所以:∠OEC=90度,即:OE⊥BC
因为:OE是圆O的半径,所以:BC是圆O的切线 6分
②如图,连结EF 设圆O的半径为r,则OC=3-r,
在Rt∆OEC中,∠OEC=90°,所以OC2=OE2+CE2,即(3-r)2=r2+(
 )2 8分
)2 8分所以:r=1
所以:OC="2,∠OCE=30°," ∠EOC=60°
因为:三角形OEC的面积为
 ,扇形OEF的面积为
,扇形OEF的面积为
9分
所以线段CE,CF与劣弧EF所围成的图形的面积为
(1)利用中垂线作图
(2)根据CE、CF与劣弧EF所围成的图形面积=三角形OEC的面积-扇形OEF的面积求解
(2)根据CE、CF与劣弧EF所围成的图形面积=三角形OEC的面积-扇形OEF的面积求解

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目