Question

【题目】在小水池旁有一盏路灯，已知支架AB的长是0.8m，A端到地面的距离AC是4m，支架AB与灯柱AC的夹角为65°．小明在水池的外沿D测得支架B端的仰角是45°，在水池的内沿E测得支架A端的仰角是50°（点C、E、D在同一直线上），求小水池的宽DE．（结果精确到0.1m）（sin65°≈0.9，cos65°≈0.4，tan50°≈1.2）

Answer 1

【答案】：小水池的宽DE为1.7米．

【解析】

过点B作BF⊥AC于F，BG⊥CD于G，根据三角函数和直角三角形的性质解答即可．

过点B作BF⊥AC于F，BG⊥CD于G，

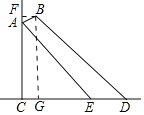
在Rt△BAF中，∠BAF=65°，BF=ABsin∠BAF=0.8×0.9=0.72，

AF=ABcos∠BAF=0.8×0.4=0.32，

∴FC=AF+AC=4.32，

∵四边形FCGB是矩形，

∴BG=FC=4.32，CG=BF=0.72，

∵∠BDG=45°，

∴∠BDG=∠GBD，

∴GD=GB=4.32，

∴CD=CG+GD=5.04，

在Rt△ACE中，∠AEC=50°，CE=≈3.33，

∴DE=CD-CE=5.04-3.33=1.71≈1.7，

答：小水池的宽DE为1.7米．