题目内容
【题目】已知等腰三角形ABC的底边BC=20cm,D是腰AB上一点,且CD=16cm,BD=12cm
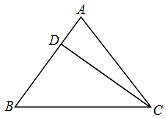
(1)请判断CD与AB的位置关系,并说明理由;
(2)求该三角形的腰的长度.
【答案】(1) CD⊥AB,见解析;(2)腰长为![]() cm.
cm.
【解析】
(1)依据勾股定理的逆定理,即可得到∠BDC=90°,即可得到CD⊥AB;
(2)设腰长为x,则AD=x-12,由(1)可知AD2+CD2=AC2,解方程(x-12)2+162=x2,即可得到腰长.
解:(1)CD⊥AB
理由:∵BC=20cm,CD=16cm,BD=12cm,
∴BD=144;CD=256;BC=400
∴BD2+CD2=BC2,
∴根据勾股定理逆定理可知,∠BDC=90°,
即CD⊥AB;
(2)设腰长为x,则AD=x﹣12,
由(1)可知AD2+CD2=AC2,
即:(x﹣12)2+162=x2,
解得x=![]() ,
,
∴腰长为![]() cm.
cm.

练习册系列答案
相关题目