Question

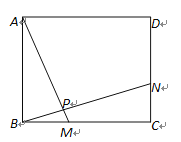
【题目】如图1，正方形ABCD的边长为4，对角线AC、BD交于点M．

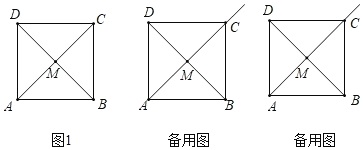
（1）直接写出AM=　　　　；

（2）P是射线AM上的一点，Q是AP的中点，设PQ=x．

①AP=　　　　 ，AQ=　　　　 ；

②以PQ为对角线作正方形，设所作正方形与△ABD公共部分的面积为S，用含x的代数式表示S，并写出相应的x的取值范围．(直接写出，不需要写过程)

Answer 1

【答案】（1）；（2）①2x，x；②S(0＜x≤)．

【解析】

（1）根据勾股定理可得AC=，进而根据正方形对角线相等而且互相平分，可得AM的长；

（2）由中点定义可得AP=2PQ，AQ=PQ，然后由正方形与△ABD公共部分可得是以QM为高的等腰直角三角形，据此即可解答．

解：（1）∵正方形ABCD的边长为4，

∴对角线AC4，

又∴AM2．

故答案为：2．

（2）①Q是AP的中点，设PQ=x，

∴AP=2PQ=2x，AQ=x．

故答案为：2x；x．

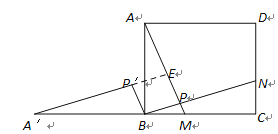
②如图：

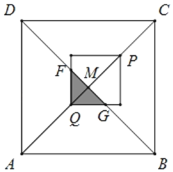
∵以PQ为对角线作正方形，

∴∠GQM=∠FQM=45°

∵正方形ABCD对角线AC、BD交于点M，

∴∠FMQ=∠GMQ=90°，

∴△FMQ和△GMQ均为等腰直角三角形，

∴FM=QM=MG．

∵QM=AM﹣AQ=2x，

∴SFGQM，

∴S，

∵依题意得：，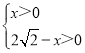

∴0＜x≤2，

综上所述：S(0＜x≤2)，