题目内容
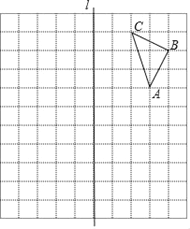
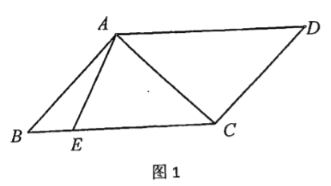
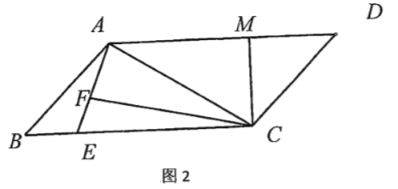
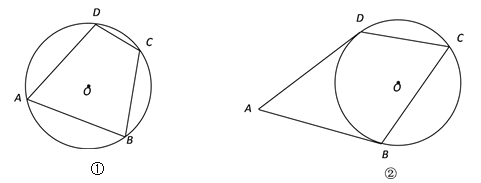
【题目】如图,正方形ABCD中,点E是AD边的中点,BD,CE交于点H,BE、AH交于点G,则下列结论:①∠ABE=∠DCE;②AG⊥BE;③S△BHE=S△CHD;④∠AHB=∠EHD.其中正确的是( )
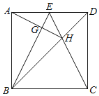
A.①③B.①②③④C.①②③D.①③④
【答案】B
【解析】
根据正方形的性质证得△BAE≌△CDE,推出∠ABE=∠DCE,可知①正确;利用正方形性质证△ADH≌△CDH,求得∠HAD=∠HCD,推出∠ABE=∠HAD;求出∠ABE+∠BAG=90°;最后在△AGE中根据三角形的内角和是180°求得∠AGE=90°即可得到②正确.根据AD∥BC,求出S△BDE=S△CDE,推出S△BDES△DEH=S△CDES△DEH,即:S△BHE=S△CHD,故③正确;由∠AHD=∠CHD,得到邻补角和对顶角相等得到∠AHB=∠EHD,故④正确;
解:∵四边形ABCD是正方形,E是AD边上的中点,
∴AE=DE,AB=CD,∠BAD=∠CDA=90°,
∴△BAE≌△CDE(SAS),
∴∠ABE=∠DCE,
故①正确;
∵四边形ABCD是正方形,
∴AD=DC,∠ADB=∠CDB=45°,DH=DH,
∴△ADH≌△CDH(SAS),
∴∠HAD=∠HCD,
∵∠ABE=∠DCE
∴∠ABE=∠HAD,
∵∠BAD=∠BAH+∠DAH=90°,
∴∠ABE+∠BAH=90°,
∴∠AGB=180°90°=90°,
∴AG⊥BE,
故②正确;
∵AD∥BC,
∴S△BDE=S△CDE,
∴S△BDES△DEH=S△CDES△DEH,
即:S△BHE=S△CHD,
故③正确;
∵△ADH≌△CDH,
∴∠AHD=∠CHD,
∴∠AHB=∠CHB,
∵∠BHC=∠DHE,
∴∠AHB=∠EHD,
故④正确;
故选:B.

 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案【题目】有这样一个问题:探究函数y=![]() 的图象与性质.小美根据学习函数的经验,对函数y=
的图象与性质.小美根据学习函数的经验,对函数y=![]() 的图象与性质进行了探究下面是小美的探究过程,请补充完整:
的图象与性质进行了探究下面是小美的探究过程,请补充完整:
(1)函数y=![]() 的自变量x的取值范围是 ;
的自变量x的取值范围是 ;
(2)下表是y与x的几组对应值.
x | -2 | - | -1 | - |
|
| 1 | 2 | 3 | 4 | … |
y | 0 | - | -1 | - |
|
| td style="width:28.95pt; border-top-style:solid; border-top-width:0.75pt; border-right-style:solid; border-right-width:0.75pt; border-left-style:solid; border-left-width:0.75pt; padding:3.38pt 5.03pt; vertical-align:middle">m |
|
| … |
求m的值;
(3)如图,在平面直角坐标系xOy中,描出了以上表中各对对应值为坐标的点.根据描出的点,画出该函数的图象;

(4)结合函数的图象,写出该函数的一条性质: .