ЬтФПФкШн
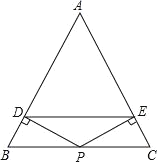
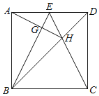
ЁОЬтФПЁПдкЦНУцжБНЧзјБъЯЕжаЃЌНЋвЛПщЕШбќжБНЧШ§НЧАхЃЈЁїABCЃЉАДШчЭМЫљЪОЗХжУЃЌШєAOЃН2ЃЌOCЃН1ЃЌЁЯACBЃН90ЁуЃЎ
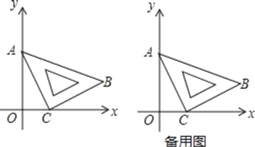
ЃЈ1ЃЉжБНгаДГіЕуBЕФзјБъЪЧЁЁ ЃЛ
ЃЈ2ЃЉШчЙћХзЮяЯпlЃКyЃНax2ЉaxЉ2ОЙ§ЕуBЃЌЪдЧѓХзЮяЯпlЕФНтЮіЪНЃЛ
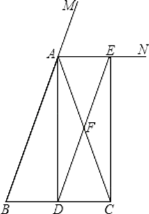
ЃЈ3ЃЉАбЁїABCШЦзХЕуCФцЪБеыа§зЊ90ЁуКѓЃЌЖЅЕуAЕФЖдгІЕуA1ЪЧЗёдкХзЮяЯпlЩЯЃПЮЊЪВУДЃП
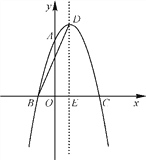
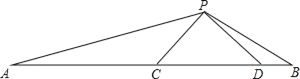
ЃЈ4ЃЉдкxжсЩЯЗНЃЌХзЮяЯпlЩЯЪЧЗёДцдквЛЕуPЃЌЪЙгЩЕуAЃЌCЃЌBЃЌPЙЙГЩЕФЫФБпаЮЮЊжааФЖдГЦЭМаЮЃПШєДцдкЃЌЧѓГіЕуPЕФзјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ЁОД№АИЁПЃЈ1ЃЉЕуBЕФзјБъЮЊЃЈ3ЃЌ1ЃЉЃЛЃЈ2ЃЉyЃН![]() x2Љ
x2Љ![]() xЉ2ЃЛЃЈ3ЃЉЕуA1дкХзЮяЯпЩЯЃЛРэгЩМћНтЮіЃЛЃЈ4ЃЉДцдкЃЌЕуPЃЈЉ2ЃЌ1ЃЉЃЎ
xЉ2ЃЛЃЈ3ЃЉЕуA1дкХзЮяЯпЩЯЃЛРэгЩМћНтЮіЃЛЃЈ4ЃЉДцдкЃЌЕуPЃЈЉ2ЃЌ1ЃЉЃЎ
ЁОНтЮіЁП
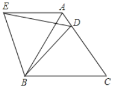
ЃЈ1ЃЉЪзЯШЙ§ЕуBзїBDЁЭxжсЃЌДЙзуЮЊDЃЌЭЈЙ§жЄУїЁїBDCЁеЁїCOAМДПЩЕУBDЃНOCЃН1ЃЌCDЃНOAЃН2ЃЌДгЖјЕУжЊBзјБъЃЛ
ЃЈ2ЃЉРћгУД§ЖЈЯЕЪ§ЗЈЃЌНЋBзјБъДњШыМДПЩЧѓЕУЃЛ
ЃЈ3ЃЉЛГіа§зЊКѓЕФЭМаЮЃЌЙ§Еу![]() зїxжсЕФДЙЯпЃЌЙЙдьШЋЕШШ§НЧаЮЃЌЧѓГі
зїxжсЕФДЙЯпЃЌЙЙдьШЋЕШШ§НЧаЮЃЌЧѓГі![]() ЕФзјБъДњШыХзЮяЯпНтЮіЪНМДПЩНјааХаЖЯЃЛ
ЕФзјБъДњШыХзЮяЯпНтЮіЪНМДПЩНјааХаЖЯЃЛ
ЃЈ4ЃЉгЩХзЮяЯпЕФНтЮіЪНЯШЩшГіPЕФзјБъЃЌдйИљОнжааФЖдГЦЕФаджЪ гыЯпЖЮжаЕуЕФЙЋЪНСаГіЗНГЬЧѓНтМДПЩЁЃ
ЃЈ1ЃЉШчЭМ1ЃЌЙ§ЕуBзїBDЁЭxжсЃЌДЙзуЮЊDЃЌ
ЁпЁЯBCD+ЁЯACOЃН90ЁуЃЌЁЯAC0+ЁЯOACЃН90ЁуЃЌ
ЁрЁЯBCDЃНЁЯCAOЃЌ
гжЁпЁЯBDCЃНЁЯCOAЃН90ЁуЃЌCBЃНACЃЌ
дкЁїBDCКЭЁїCOAжаЃК
ЁпЁЯBDC=ЁЯCOAЃЌЁЯBCDЃНЁЯCAOЃЌCB=ACЃЌ
ЁрЁїBDCЁеЁїCOAЃЈAASЃЉЃЌ
ЁрBDЃНOCЃН1ЃЌCDЃНOAЃН2ЃЌ
ЁрЕуBЕФзјБъЮЊЃЈ3ЃЌ1ЃЉЃЛ
ЃЈ2ЃЉЁпХзЮяЯпyЃНax2ЉaxЉ2Й§ЕуBЃЈ3ЃЌ1ЃЉЃЌ
Ёр1ЃН9aЉ3aЉ2ЃЌ
НтЕУЃКaЃН![]() ЃЌ
ЃЌ
ЁрХзЮяЯпЕФНтЮіЪНЮЊyЃН![]() x2Љ
x2Љ![]() xЉ2ЃЛ
xЉ2ЃЛ
ЃЈ3ЃЉа§зЊКѓШчЭМ1ЫљЪОЃЌЙ§ЕуA1зїA1MЁЭxжсЃЌ
ЁпАбЁїABCШЦзХЕуCФцЪБеыа§зЊ90ЁуЃЌ
ЁрЁЯABCЃНЁЯA1BCЃН90ЁуЃЌ
ЁрA1ЃЌBЃЌCЙВЯпЃЌ
дкШ§НЧаЮBDCКЭШ§НЧаЮA1CMжаЃК
ЁпЁЯBDC=ЁЯA1MC=90ЁуЃЌЁЯBCD=ЁЯA1CMЃЌA1C=BC,
ЁрЁїBDCЁеЁїA1CM
ЁрCMЃНCDЃН3Љ1ЃН2ЃЌA1MЃНBDЃН1ЃЌ
ЁрOMЃН1ЃЌ
ЁрЕуA1ЃЈЉ1ЃЌЉ1ЃЉЃЌ
АбЕуxЃНЉ1ДњШыyЃН![]() x2Љ
x2Љ![]() xЉ2ЃЌ
xЉ2ЃЌ
yЃНЉ1ЃЌ
ЁрЕуA1дкХзЮяЯпЩЯЃЎ
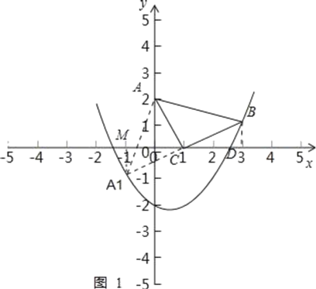
ЃЈ4ЃЉЩшЕуPЃЈtЃЌ![]() t2Љ
t2Љ![]() tЉ2ЃЉЃЌ
tЉ2ЃЉЃЌ
ЕуAЃЈ0ЃЌ2ЃЉЃЌЕуCЃЈ1ЃЌ0ЃЉЃЌЕуBЃЈ3ЃЌ1ЃЉЃЌ
ШєЕуPКЭЕуCЖдгІЃЌгЩжааФЖдГЦЕФаджЪКЭЯпЖЮжаЕуЙЋЪНПЩЕУЃК
![]() ЃЌ
ЃЌ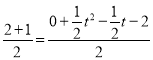 ЃЌ
ЃЌ
ЮоНтЃЌ
ШєЕуPКЭЕуAЖдгІЃЌгЩжааФЖдГЦЕФаджЪКЭЯпЖЮжаЕуЙЋЪНПЩЕУЃК
![]() ЃЌ
ЃЌ ЃЌ
ЃЌ
ЮоНтЃЌ
ШєЕуPКЭЕуBЖдгІЃЌгЩжааФЖдГЦЕФаджЪКЭЯпЖЮжаЕуЙЋЪНПЩЕУЃК
![]() ЃЌ
ЃЌ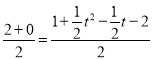 ЃЌ
ЃЌ
НтЕУЃКtЃНЉ2ЃЌ
![]() t2Љ
t2Љ![]() tЉ2ЃН1
tЉ2ЃН1
ЫљвдЃКДцдкЃЌЕуPЃЈЉ2ЃЌ1ЃЉЃЎ

 ЦпаЧЭМЪщПкЫуЫйЫуЬьЬьСЗЯЕСаД№АИ
ЦпаЧЭМЪщПкЫуЫйЫуЬьЬьСЗЯЕСаД№АИ ГѕжабЇвЕПМЪдЕМгыСЗЯЕСаД№АИ
ГѕжабЇвЕПМЪдЕМгыСЗЯЕСаД№АИ