题目内容
【题目】已知⊙O,请用无刻度的直尺完成下列作图.
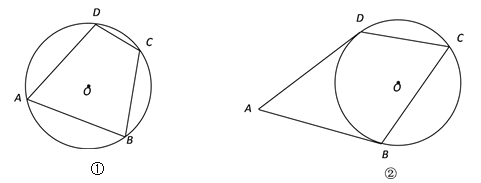
(1)如图①,四边形ABCD是⊙O的内接四边形,且AB=AD,画出∠BCD的角平分线;
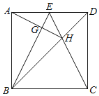
(2)如图②,AB和AD是⊙O的切线,切点分别是B、D,点C在⊙O上,画出∠BCD的角平分线.
【答案】(1)见解析;(2)见解析.
【解析】
(1)根据同圆或等圆中,相等的弦所对的弧相等,同弧或等弧所对的圆周角相等,连接AC即为所求;
(2)根据切线长定理,圆外一点可以引圆的两条切线,这一点到切点的距离相等,这一点和圆心的连线平分两条切线的夹角,再利用相等的圆心角所对的弧相等,同弧所对的圆周角相等,连接EC即为所求.
解:(1)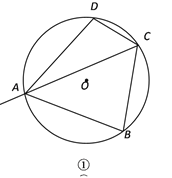
∵四边形ABCD是⊙O的内接四边形,且AB=AD
∴![]() ∴∠DAC=∠BAC
∴∠DAC=∠BAC
∴连接AC即为所求
(2)
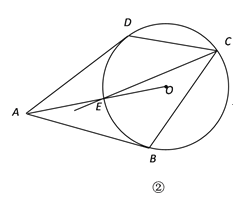
∵AB和AD是⊙O的切线,切点分别是B、D,
连接AO,交圆O于点E,根据切线长定理可知AB=AD,∠DAO=∠BAO,又∵AO=AO,∴△ADO≌△ABO,∴∠AOD=∠AOB,即![]()
∴连接CE即为所求.

练习册系列答案
相关题目