��Ŀ����
����Ŀ������ʱ���������뵽�ķ���δ������ģ����������һ�룬�����Ż��ⷨ��
�������
����x�ķ���a(x��m)2��b��0�Ľ���x1��1��x2����2��a��m��b��Ϊ������a��0������a(x��m��2)2��b��0�Ľ����� ��
�ⷨ̽��
��1��С����˼·��ͼ��ʾ�����㰴������˼·���������⣻
С����˼·
��1�� ��1����2���뵽��1�����������m��ֵ��
��2�� ��m��ֵ���뵽��1�����������![]() ��ֵ��
��ֵ��
��3�� ���2�����̣�
��2��С����ϸ�۲��������̣����ѵ�2������a(x��m��2)2��b��0�еġ�x��2��������1�������еġ�x������x��2����ֵΪ�� ���Ӷ����ؽ�������⣮
��������
��3��С����С������˼�����֣����÷��̽ṹ���ص㣬������㡰�����б�ʽ���������ɽ���������⣬��������˵�ķ�����ɽ��
��֪���� (a2��2b2)x2��(2b2��2c2)x��2c2��a2��0��������ȵ�ʵ����������a��b��c�ǡ�ABC���ߵij����жϡ�ABC����״��
���𰸡���1��x1����1��x2����4 ��2��1��2 ��3��ֱ��������
��������
��1�������������ô���ϵ������⼴��.
��2���Ѻ���һ�������е�x+2�������壬�൱��ǰ��һ�������е�x��⣮
��3���ȸ�����������ȵ�ʵ�������ٸ��ݸ���ϵ���Ĺ�ϵ�г����̣��ҵ�a��b��c�Ĺ�ϵ���Ӷ��ж������ε���״��
��1���⣺��x1��1��x2����2���뵽����a(x��m)2��b��0�У�
��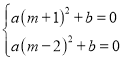 ��
��
�� m��1����(m��2)��
��� m��![]()
�� a(![]() ��1)2��b��0��
��1)2��b��0��
�� ��![]() ��
��![]()
��2�����̿ɱ���Ϊ(x��![]() ��2)2����
��2)2����![]() ��
��
��(x��![]() )2��
)2��![]() ��
��
��ã�x1����1��x2����4
��2������x�ķ���a��x+m��2+b=0�Ľ���x1=-2��x2=1����a��m��b��Ϊ������a��0����
��3���⣺�� (a2��2b2)��(2b2��2c2)��(2c2��a2)��0��
�� ���̱���һ����x��1
�� ���̵�����Ϊx1��x2��1��
�� x1��x2��1��![]() ��
��
�� a2��b2��c2��
�� ��ABC��һ��ֱ��������