题目内容
【题目】如图,∠MON=45°,线段AB在射线ON上运动,AB=2.
(1)如图1,已知OA=AB,AC=BC,∠ACB=90°,点C在∠MON内.
①求证:以点C为圆心,CA的半径的圆与射线OM相切(切点记为点P);
②∠APB的大小为 .
(2)如图2,若射线OM上存在点Q,使得∠AQB=30度,试利用图2,求A,O两点之间距离t的取值范围.

【答案】(1)① 见解析,②45°;(2)0≤t≤2![]() -1
-1
【解析】
(1)①如图1中,作CP⊥OM于P,AH⊥OM于H.证明CP=AC即可.
②利用圆周角定理解决问题即可.
(2)如图3中,以AB为边向上作等边△ABC,以C为圆心CA为半径作⊙C,当⊙C与射线OM有交点时,射线OM上存在点Q,使得∠AQB![]() ∠ACB=30°.当⊙C与射线OM相切于点Q时,作CP∥OM交OB于P,作PK⊥OM于K,则四边形CQKP是矩形,解直角三角形求出OA的值即可判断.
∠ACB=30°.当⊙C与射线OM相切于点Q时,作CP∥OM交OB于P,作PK⊥OM于K,则四边形CQKP是矩形,解直角三角形求出OA的值即可判断.
(1)①如图1中,作CP⊥OM于P,AH⊥OM于H.
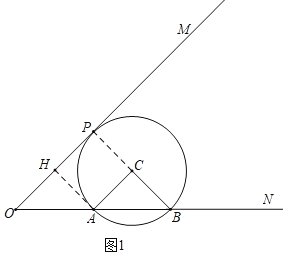
∵CA=CB,∠ACB=90°,∴∠CAB=45°.
∵∠O=45°,∴∠CAB=∠O,∴AC∥OP.
∵PC∥AH,∴四边形ACPH是平行四边形.
∵∠CPH=90°,∴四边形ACPH是矩形.
∵OA=AB,∠AHO=∠BCA=90°,∠O=∠CAB=45°,
∴△AOH≌△BAC(AAS),∴AC=BC=OH=AH,
∴四边形ACPH是正方形,∴PC=AC,∴OM是⊙C的切线.
②如图2中,连接PA.
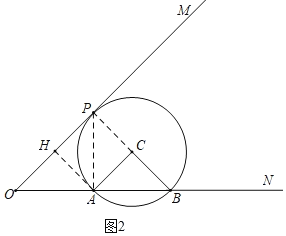
由①可知四边形ACPH是正方形,∴∠ACP=90°.
∵∠ACB=90°,∴∠PCB=180°,∴P,C,B共线,
∴∠APB![]() ∠ACB=45°.
∠ACB=45°.
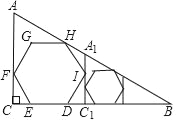
(2)如图3中,以AB为边向上作等边△ABC,
以C为圆心CA为半径作⊙C,当⊙C与射线OM有交点时,
射线OM上存在点Q,使得∠AQB![]() ∠ACB=30°.
∠ACB=30°.
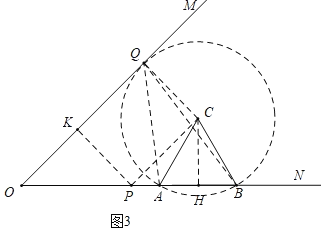
当⊙C与射线OM相切于点Q时,作CP∥OM交OB于P,
作PK⊥OM于K,则四边形CQKP是矩形,
∴PK=CQ=CA=AB=2.
∵∠O=45°,∠OKP=90°,∴OK=PK=2,
∴OP![]() OK=2
OK=2![]() .
.
过C作CH⊥AB于H.
∵△ABC是等边三角形,CH⊥AB,
∴AH=HB=1,CH![]() ,
,
∴PC∥OM,∴∠CPH=∠O=45°,∴PH=CH![]() ,
,
∴OH=OP+PH=2![]() ,∴OA=OH-AH=2
,∴OA=OH-AH=2![]() 1,
1,
观察图形可知,满足条件的t的取值范围为:0≤t≤2![]() 1.
1.

【题目】为了解今年我校初三学生中考体育测试成绩,现对今年我校初三中考体育测试成绩进行抽样调查,结果统计如下,其中扇形统计图中C组所在的扇形的圆心角为36°,组别成绩(分)频数.
组别 | 成绩(分) | 频数 |
A | 30<x≤34 | 1 |
B | 34<x≤38 | 1 |
C | 38<x≤42 | 6 |
D | 42<x≤46 | b |
E | 46<x≤50 | 30 |
合计 | a | |
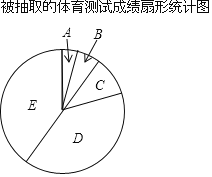
根据上面图标提供的信息,回答下列问题:
(1)计算频数分布表中a与b的值;
(2)根据C组38<x≤42的组中间值40,估计C组中所有数据的和为 ;
(3)请估计今年我校初三学生中考体育成绩的平均分(结果取整数).