题目内容
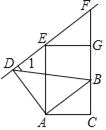
【题目】如图，Rt△ABC中，∠C＝Rt∠，AB＝2，∠B＝30°，正六边形DEFGHI完全落在Rt△ABC内，且DE在BC边上，F在AC边上，H在AB边上，则正六边形DEFGHI的边长为_____，过I作A1C1∥AC，然后在△A1C1B内用同样的方法作第二个正六边形，按照上面的步骤继续下去，则第n个正六边形的边长为_____．
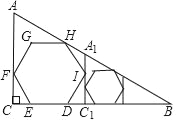
【答案】
， （
）n﹣1×（）n．
【解析】
如图，连接AG，延长HG交AC于J．则易知AJ＝JF＝CF，设EF＝a，则EC＝
a，CF＝
a．构建方程求出a，探究规律利用规律即可解决问题；
解：如图，连接AG，延长HG交AC于J．则易知AJ＝JF＝CF，设EF＝a，则EC＝a，CF＝a．
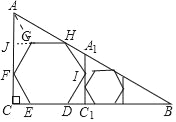
∴3CF＝AC，
∴a＝AC，
在Rt△ABC中，∵AB＝2，∠B＝30°，
∴AC＝AB＝1，
∴a＝，
易知A1C1＝
a，
∴第二个正六边形边长为： ××＝（）1×（）2，
同法可得第三个正六边形的边长为：＝（）2×（）3，
∴第n个正六边形的边长为：（）n﹣1×（）n，
故答案为：，（）n﹣1×（）n；
练习册系列答案
阅读快车系列答案
相关题目
【题目】近年来，“在初中数学教学候总使用计算器是否直接影响学生计算能力的发展”这一问题受到了广泛关注，为此，某校随机调查了n名学生对此问题的看法（看法分为三种：没有影响，影响不大，影响很大），并将调查结果 绘制成如下不完整的统计表和扇形统计图，根据统计图表提供的信息，解答下列问题：
n名学生对使用计算器影响计算能力的发展看法人数统计表
看法 | 没有影响 | 影响不大 | 影响很大 |
学生人数（人） | 40 | 60 | m |
（1）求n的值；
（2）统计表中的m= ；
（3）估计该校1800名学生中认为“影响很大”的学生人数．
