Question

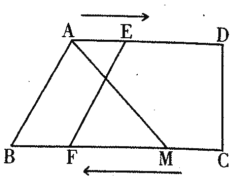
【题目】如图，在△ABC中，，CD平分交AB于点D，将△CDB绕点C顺时针旋转到△CEF的位置，点F在AC上.

（1）△CDB旋转了________度；

（2）连结DE，判断DE与BC的位置关系，并说明理由.

Answer 1

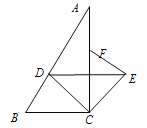
【答案】90

【解析】（1）由旋转的性质可得结论；

（2）由角平分线的定义得到∠BCD=∠ACD=45°．由旋转的性质得到CD=CE，∠BCD=∠ECA=45°，故∠DCE=90°，∠CED=45°，∠ECD=45°，得到∠DCB=∠EDC，由内错角相等，两直线平行即可得到结论．

（1）由旋转的性质可知：旋转角为∠BCA=90°．故答案为：90°．

（2）DE//BC．理由如下：

∵CD平分∠ACD， ∠ACB=90°，

∴∠BCD=∠ACD=45°．

又∵ΔCDB绕点C顺时针旋转到ΔCEF，

∴CD=CE，∠BCD=∠ECA=45°；

∴∠DCE=90°，∠CED=45°；

∴∠ECD=45°，

∴∠DCB=∠EDC，

∴DE//BC．