题目内容
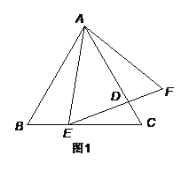
【题目】如图，在大楼AB正前方有一斜坡CD，坡角∠DCE=30°，楼高AB=60米，在斜坡下的点C处测得楼顶B的仰角为60°，在斜坡上的D处测得楼顶B的仰角为45°，其中点A,C,E在同一直线上.
（1）求坡底C点到大楼距离AC的值；
（2）求斜坡CD的长度.
【答案】（1）坡底C点到大楼距离AC的值为20
米；（2）斜坡CD的长度为80-120米.
【解析】（1）在直角三角形ABC中，利用锐角三角函数定义求出AC的长即可；
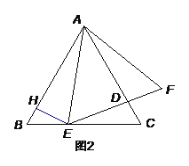
（2）过点D作DF⊥AB于点F，则四边形AEDF为矩形，得AF=DE，DF=AE.利用DF=AE=AC+CE求解即可.
（1）在直角△ABC中，∠BAC=90°，∠BCA=60°，AB=60米，则AC=
（米）
答：坡底C点到大楼距离AC的值是20米．
（2）过点D作DF⊥AB于点F，则四边形AEDF为矩形，
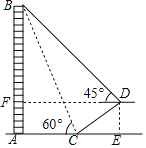
∴AF=DE，DF=AE.
设CD=x米，在Rt△CDE中，DE=
x米，CE=
x米
在Rt△BDF中，∠BDF=45°，
∴BF=DF=AB-AF=60-x（米）
∵DF=AE=AC+CE，
∴20+x=60-x
解得：x=80-120（米）
故斜坡CD的长度为（80-120）米.
练习册系列答案
相关题目
【题目】将长为
，宽为
的长方形白纸，按图示方法粘合起来，粘合部分宽为
．
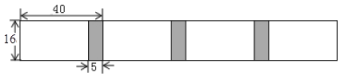
（1）根据图示，将下表补充完整；
白纸张数 | 1 | 2 | 3 | 4 | 5 | … |
纸条长度/ | 40 | 110 | 145 | … |
（2）设
张白纸粘合后的总长度为
，求与之间的关系式；
（3）将若干张白纸按上述方式粘合起来，你认为总长度可能为
吗？为什么？
