Question

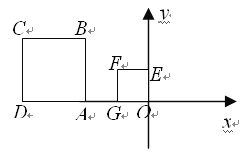
【题目】如图，在平面直角坐标系中，正方形ABCD的边长为2，正方形EFGH的边长为5，点A的坐标为（﹣4，0），点E的坐标为（3，0），AB与EF均在x轴上．

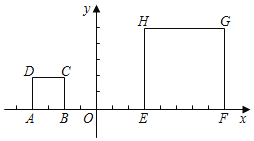
（1）C，G两点的坐标分别为　 　，　 　．

（2）将正方形ABCD绕点E顺时针旋转90°得到正方形A'B'C'D'，求点C'的坐标和FC'的长．

Answer 1

【答案】（1）（﹣2，2），（8，5）；（2）C'（5，5），

【解析】

（1）由正方形的性质可得点B（﹣2，0），BC=AB=2，点F（8，0），EF=GF=5，即可求解；

（2）画出旋转后的图形，可得C'的坐标，由勾股定理可求FC'的长．

（1）∵正方形ABCD的边长为2，正方形EFGH的边长为5，

点A的坐标为（﹣4，0），点E的坐标为（3，0），

∴点B（﹣2，0），BC=AB=2，点F（8，0），EF=GF=5，

∴点C坐标（﹣2，2），点G（8，5）

故答案为：（﹣2，2），（8，5）；

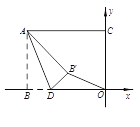
（2）如图，将正方形ABCD绕点E顺时针旋转90°得到正方形A'B'C'D'，

此时点H与点B'重合，

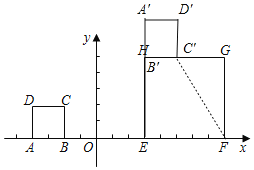
∴点C'（5，5）．

∵C'G=B'G﹣B'C'=3，GF=5，

∴C'F===．