题目内容
【题目】已知一次函数y=![]() x12的图象分别交x轴,y轴于A,C两点。
x12的图象分别交x轴,y轴于A,C两点。
(1)求出A,C两点的坐标;
(2)在x轴上找出点B,使△ACB∽△AOC,若抛物线过A,B,C三点,求出此抛物线的解析式;
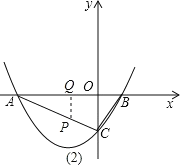
(3)在(2)的条件下,设动点P、Q分别从A,B两点同时出发,以相同速度沿AC、BA向C,A运动,连接PQ,设AP=m,是否存在m值,使以A,P,Q为顶点的三角形与△ABC相似?若存在,求出所有m值;若不存在,请说明理由。
【答案】(1)A(16,0),C(0,12);(2)![]() ;(3)
;(3)![]()
【解析】
(1)令直线的解析式y=0,可得A的坐标,令x=0,可得C的坐标
(2)要使△ACB∽△AOC,则B点必为过C点且垂直于AC的直线与x轴的交点.那么根据射影定理不难得出B点的坐标,然后用待定系数法即可求得抛物线的解析式.
(3)本题可分两种情况进行求解:①当PQ∥BC时,△APQ∽△ACB;②当PQ⊥AB时,△APQ∽△ACB.可根据各自得出的不同的对应成比例线段求出m的值.
(1)在一次函数y=![]() x12中,当x=0时,y=12;
x12中,当x=0时,y=12;
当y=0时,x=16,即A(16,0),C(0,12)
(2)过C作CB⊥AC,交x轴于点B,显然,点B为所求。
则OC2=OAOB,此时OB=9,可求得B(9,0);
此时经过A. B.C三点的抛物线的解析式为y=![]() x2+
x2+![]() x12
x12
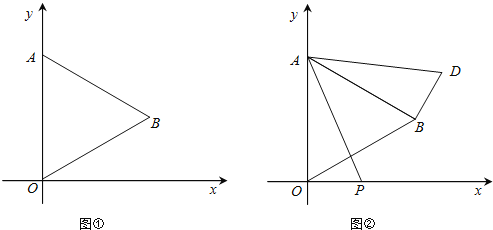
(3)当PQ∥BC时,如图(1),△APQ∽△ACB;则有:
![]() =
=![]() ,即
,即![]() =
=![]() ,
,
解得m=![]() .
.
当PQ⊥AB时,△APQ∽△ACB;有:
![]() =
= ![]() ,即
,即![]() =
=![]() ,
,
解得m=![]() .
.

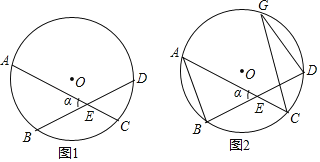
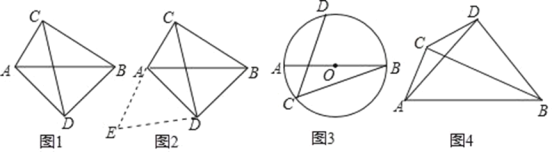
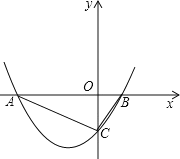
【题目】如图1,圆O的两条弦AC、BD交于点E,两条弦所成的锐角或者直角记为∠α
(1)点点同学通过画图和测量得到以下近似数据:
| 30.2° | 40.4° | 50.0° | 61.6° |
| 55.7° | 60.4° | 80.2° | 100.3° |
∠α的度数 | 43.0° | 50.2° | 65.0° | 81.0° |
猜想:![]() 、
、![]() 、∠α的度数之间的等量关系,并说明理由﹒
、∠α的度数之间的等量关系,并说明理由﹒
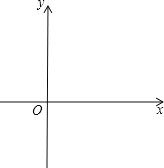
(2)如图2,若∠α=60°,AB=2,CD=1,将以![]() 圆心为中心顺时针旋转,直至点A与点D重合,同时B落在圆O上的点,连接CG﹒
圆心为中心顺时针旋转,直至点A与点D重合,同时B落在圆O上的点,连接CG﹒
①求弦CG的长;
②求圆O的半径.