题目内容
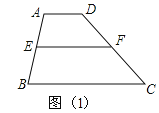
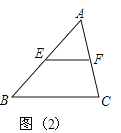
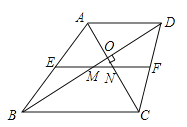
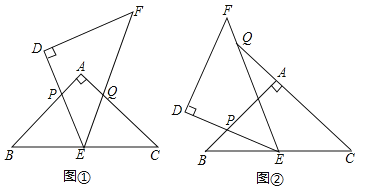
【题目】(2017甘肃省天水市)△ABC和△DEF是两个全等的等腰直角三角形,∠BAC=∠EDF=90°,△DEF的顶点E与△ABC的斜边BC的中点重合,将△DEF绕点E旋转,旋转过程中,线段DE与线段AB相交于点P,线段EF与射线CA相交于点Q.
(1)如图①,当点Q在线段AC上,且AP=AQ时,求证:△BPE≌△CQE;
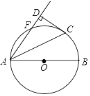
(2)如图②,当点Q在线段CA的延长线上时,求证:△BPE∽△CEQ;并求当BP=2,CQ=9时BC的长.
【答案】(1)证明见解析;(2)证明见解析,![]() .
.
【解析】
试题(1)由AB=AC,AP=AQ可得BP=CQ,又因BE=CE,∠B=∠C=45°,利用“SAS”判定△BPE≌△CQE;(2)连接PQ,根据三角形的一个外角等于与它不相邻的两个内角的和可得∠BEP+∠DEF=∠EQC+∠C,所以∠BEP=∠EQC;再由两角对应相等的两个三角形相似可得△BPE∽△CQE,根据相似三角形的性质可得![]() ,把BP=a,CQ=
,把BP=a,CQ=![]() 代入上式可求得BE=CE=
代入上式可求得BE=CE=![]() ,再求得
,再求得![]() ,AB=AC=BCsin45°=3a,所以
,AB=AC=BCsin45°=3a,所以![]() ,
,![]() ,在Rt△APQ中,由勾股定理可得
,在Rt△APQ中,由勾股定理可得![]() .
.
试题解析:
解:(1)证明:∵△ABC是等腰直角三角形,
∴∠B=∠C=45°,AB=AC,
∵AP=AQ,
∴BP=CQ,
∵E是BC的中点,
∴BE=CE,
在△BPE和△CQE中,
∵ ,
,
∴△BPE≌△CQE(SAS);
(2)解:连接PQ,

∵△ABC和△DEF是两个全等的等腰直角三角形,
∴∠B=∠C=∠DEF=45°,∵∠BEQ=∠EQC+∠C,
即∠BEP+∠DEF=∠EQC+∠C,
∴∠BEP+45°=∠EQC+45°,
∴∠BEP=∠EQC,
∴△BPE∽△CQE,
∴![]() ,
,
∵BP=a,CQ=![]() a,BE=CE,
a,BE=CE,
∴ ,
,
∴BE=CE=![]() ,
,
∴![]() ,
,
∴AB=AC=BCsin45°=3a,
∴![]() ,
,![]() ,
,
在Rt△APQ中,![]() .
.