题目内容
【题目】如图,AB为⊙O的直径,弦CD⊥AB,垂足为F,CG⊥AE,交弦AE的延长线于点G,且CG=CF.
(1)求证:CG是⊙O的切线;
(2)若AE=2,EG=1,求由弦BC和![]() 所围成的弓形的面积.
所围成的弓形的面积.

【答案】(1)见解析;(2)![]()
【解析】
(1)连接OC得∠ACO=∠BAC,证明Rt△ACG≌Rt△ACF得∠CAG=∠CAB,所以∠ACO=∠CAG,故OC∥AG,可证明∠OCG+∠G=180°,进而可得结论;
(2) 过点O作OM⊥AE,得AM=ME=1,再证明四边形OCGM为矩形得OC=2,从而可求得OF=1,进而得∠COF=60°,再根据S弓形BC=S扇形OBC- S△OBC求解即可.
(1)证明:连接OC.
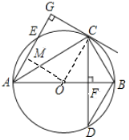
∴OA=OC
∴∠ACO=∠BAC
∵CD⊥AB,CG⊥AE,
∴∠CGA=∠CFA=90°
∵CG=CF,AC=AC
∴Rt△ACG≌Rt△ACF
∴∠CAG=∠CAB,
∴∠ACO=∠CAG
∴OC∥AG,
∴∠OCG+∠G=180°
∵∠CGA=90°
∴∠OCG=90°,即![]() ,
,
∴CG是⊙O的切线.
(2)过点O作OM⊥AE,垂足为M,
则AM=ME=![]() AE=1,∠OMG=∠OCG=∠G=90°.
AE=1,∠OMG=∠OCG=∠G=90°.
∴四边形OCGM为矩形,
∴OC=MG=ME+EG=2.
在Rt△AGC和Rt△AFC中
![]()
∴Rt△AGC≌Rt△AFC,
∴AF=AG=AE+EG=3,
∴OF=AF-OA=1,
在Rt△COF中,
∵cos∠COF=![]() =
=![]() .
.
∴∠COF=60°,CF=OC·sin∠COF=2×![]() =
=![]() ,
,
∴S弓形BC=![]() -
-![]() ×2×
×2×![]() =
=![]()

练习册系列答案
相关题目