题目内容
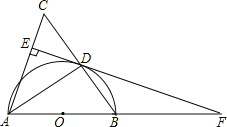
【题目】如图,已知![]() 为等边三角形,
为等边三角形,![]() ,点
,点![]() 为边
为边![]() 上一点,过点
上一点,过点![]() 作
作![]() .交
.交![]() 于
于![]() 点;过
点;过![]() 点作
点作![]() ,交
,交![]() 的延长线于
的延长线于![]() 点.设
点.设![]() ,
,![]() 的面积为
的面积为![]() ,则能大致反映
,则能大致反映![]() 与
与![]() 函数关系的图象是( )
函数关系的图象是( )
A.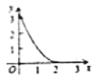 B.
B.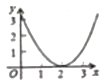
C.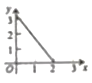 D.
D.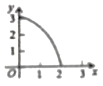
【答案】A
【解析】
根据平行线的性质可得∠EDC=∠B=60°,根据三角形内角和定理即可求得∠F=30°,然后证得△EDC是等边三角形,从而求得ED=DC=2﹣x,再根据直角三角形的性质求得EF,最后根据三角形的面积公式求得y与x函数关系式,根据函数关系式即可判定.
∵△ABC是等边三角形,
∴∠ABC=60°,
∵DE∥AB,
∴∠EDC=∠ABC=60°,
∵EF⊥DE,
∴∠DEF=90°,
∴∠F=90°﹣∠EDF=30°;
∵∠ACB=60°,∠EDB=60°,
∴△EDB是等边三角形.
∴ED=DB=2﹣x,
∵∠DEF=90°,∠F=30°,
∴EF=![]() ED=
ED=![]() (2﹣x).
(2﹣x).
∴y=![]() EDEF=
EDEF=![]() (2﹣x)
(2﹣x)![]() (2﹣x),
(2﹣x),
即y=![]() (x﹣2)2,(x<2)
(x﹣2)2,(x<2)
故选:A

练习册系列答案
相关题目
【题目】广宇、承义两名同学分别进行5次射击训练,训练成绩(单位:环)如下表:
第一次 | 第二次 | 第三次 | 第四次 | 第五次 | |
广宇 | 9 | 8 | 7 | 7 | 9 |
承义 | 6 | 8 | 10 | 8 | 8 |
对他们的训练成绩作如下分析,其中说法正确的是( )
A.广宇训练成绩的平均数大于承义训练成绩平均数
B.广宇训练成绩的中位数与承义训练成绩中位数不同
C.广宇训练成绩的众数与承义训练成绩众数相同
D.广宇训练成绩比承义训练成绩更加稳定