��Ŀ����
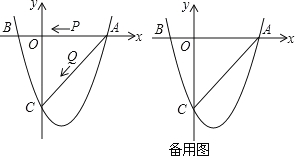
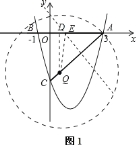
����Ŀ����ͼ�����κ���![]() ��ͼ����x�ύ��A��3��0����B����1��0�����㣬��y���ཻ�ڵ�C��0����4����
��ͼ����x�ύ��A��3��0����B����1��0�����㣬��y���ཻ�ڵ�C��0����4����
��1����ö��κ����Ľ�����
��2������P��Qͬʱ��A���������ÿ��1����λ���ȵ��ٶȷֱ���AB��AC���˶�������һ�㵽��˵�ʱ����һ��Ҳ��ֹ֮ͣ�˶���
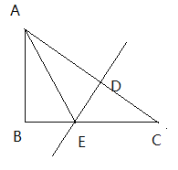
������P�˶���B��ʱ����x�����Ƿ���ڵ�E��ʹ����A��E��QΪ�����������Ϊ���������Σ������ڣ������E������ꣻ�������ڣ���˵�����ɣ�
����P��Q�˶���t��ʱ����APQ��PQ���ۣ���Aǡ��������������D�㴦����ֱ��д��t��ֵ��D������꣮
���𰸡���1��![]() ����2�����������������ĵ�E����E������Ϊ
����2�����������������ĵ�E����E������Ϊ![]() ��
��![]() ����1��0����7��0������
����1��0����7��0������![]() ��
��![]()
��������
�����������1����A��B��C��������뺯��![]() �У����b��c�������������ʽ��
�У����b��c�������������ʽ��
��2�����������������������AE=EQ��AQ=EQ��AE=AQ��������ֱƽ���ߣ���Բ��E����λ�ã���߳�Ϊx����ʾ�����ߺ����ù��ɶ�����E���ꣻ
��3��ע�P��Q�˶��ٶ���ͬ������APQ�˶�ʱ��Ϊ���������Σ�����A��D�Գƣ���AP=DP��AQ=DQ�����ı����ı߶���ȣ������Σ��������ζԱ�ƽ������ȵ����ʿ���t��ʾD�����꣬��D��E�����ϣ����Դ��뼴����t������D�ɱ�ʾ��
�����������1�������κ���![]() ��ͼ����x�ύ��A��3��0����B����1��0����C��0����4����
��ͼ����x�ύ��A��3��0����B����1��0����C��0����4����
��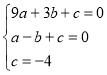 �����
����� 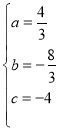 ��
��![]() ��
��
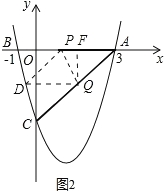
�����ڣ���ͼ1������Q��![]() ��D����ʱ
��D����ʱ![]() ����A��3��0����B����1��0����C��0����4����O��0��0����
����A��3��0����B����1��0����C��0����4����O��0��0����![]()
![]() ������P�˶���B��ʱ����Qֹͣ�˶���
������P�˶���B��ʱ����Qֹͣ�˶���![]()
![]()
![]()
![]()
![]()
![]()
������AQ�Ĵ�ֱƽ���ߣ���AO��E����ʱAE=EQ������AEQΪ���������Σ���![]() ��
��![]()
![]() ��
��![]() ��
��![]() ���
���![]()
![]()
![]() ˵����E��
˵����E��![]() ��ĸ������ϣ�������QΪԲ�ģ�AQ���뾶��Բ����
��ĸ������ϣ�������QΪԲ�ģ�AQ���뾶��Բ����![]() ����E����ʱ
����E����ʱ![]()
![]()
![]() 1.
1.![]()
![]() ������
������![]() ʱ��2.��E��A�����ʱ��
ʱ��2.��E��A�����ʱ��![]()
![]() 2����E��A���ұ�ʱ��
2����E��A���ұ�ʱ��![]()
![]() �����������������������ĵ�E����E������Ϊ
�����������������������ĵ�E����E������Ϊ![]() ��
��![]() ����1��0����7��0����
����1��0����7��0����
����ͼ2��D�����PQ��A��Գƣ�����Q����![]() ��F��
��F��![]()
![]()
![]() ���ı���AQDPΪ���Σ�
���ı���AQDPΪ���Σ�![]()
![]()
![]()
![]()
![]()
![]()
![]() ��D�ڶ��κ���
��D�ڶ��κ���
![]() �ϣ�
�ϣ�![]()
![]() ��
��![]() ����A�غϣ���ȥ����
����A�غϣ���ȥ����![]()

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�����Ŀ���±��ǹ�������뱱����ʱ�� �������ŵ�����ʾͬһʱ�̱ȱ���ʱ�����ʱ����
���� | ŦԼ | ���� | ���� | ���� |
ʱ�ʱ�� | ��13 | ��7 | +1 | ��12 |
������ڶ���ʱ����16��00����ôŦԼʱ����__�������Ͼ�Ϊ24Сʱ�ƣ�