��Ŀ����
����Ŀ�����ž��õĿ��ٷ�չ����������Խ��Խ�ܵ����ǵĹ�ע��ijУѧ����Ϊ���˽���������֪ʶ���ռ��������������˲���ѧ������������Ϊ���dz��˽������˽������˽�����������˽������࣬�������������Ƴ���������ͳ��ͼ��

��1�����α������ѧ���ж���������ȫ����ͳ��ͼ��
��2�����Ƹ�У1200��ѧ�������dz��˽��������˽������������Ƕ��٣�
��3������������dz��˽�����ѧ������2������������ΪŮ�������������ȡ2����ȫУ����������֪ʶ�����������û���״ͼ���б��ķ�������ǡ�ó鵽һ��һŮ�ĸ��ʣ�
���𰸡���1�����α������ѧ����50�ˣ���ȫͼ�μ���������2�����Ƹ�У1200��ѧ�������dz��˽��������˽�������������408�ˣ���3��ǡ�ó鵽һ��һŮ�ĸ���Ϊ![]() ��
��
��������
��1�������˽���������������ռ�ٷֱ���������������������Զ�Ӧ�İٷֱȿ�������dz��˽��������˽���������������̶���������˽������������Ӷ���ȫͼ�Σ�
��2������������������˼�����ɵã�
��3������״ͼչʾ����20�ֵȿ��ܵĽ���������ҳ����������Ľ������Ȼ�����ø��ʹ�ʽ��⣮
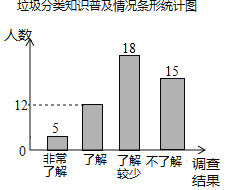
��1�����α������ѧ������12��24%��50���ˣ���
�����dz��˽���������Ϊ50��10%��5���ˣ���
���˽������������Ϊ50��36%��18���ˣ���
�����˽���������Ϊ50����5+12+18����15���ˣ���
��ȫͼ�����£�
��2�����Ƹ�У1200��ѧ�������dz��˽��������˽�������������1200��![]() ��408���ˣ���
��408���ˣ���
��3������״ͼΪ��
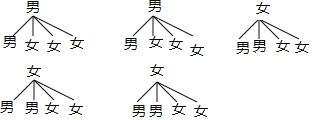
����20�ֵȿ��ܵĽ����������ǡ�ó鵽һ��һŮ����12�ֽ����
����ǡ�ó鵽һ��һŮ�ĸ���Ϊ![]() ��
��![]() ��
��

 ��У����ϵ�д�
��У����ϵ�д�




