题目内容
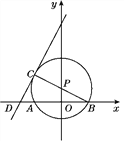
【题目】如图,四边形ABCD是菱形,AB=2,且∠ABC=∠ABE=60°,M为对角线BD(不含B点)上任意一点,将BM绕点B逆时针旋转60°得到BN,连接EN、AM、CM,则AM+BM+CM的最小值为_________.

【答案】![]()
【解析】
根据“两点之间线段最短”,当M点位于BD与CE的交点处时,AM+BM+CM的值最小,即等于EC的长.
如图,连接MN,

∵△ABE是等边三角形,
∴BA=BE,∠ABE=60°.
∵∠MBN=60°,
∴∠MBN-∠ABN=∠ABE-∠ABN.
即∠MBA=∠NBE.
又∵MB=NB,
∴△AMB≌△ENB(SAS),
∴AM=EN,
∵∠MBN=60°,MB=NB,
∴△BMN是等边三角形.
∴BM=MN.
∴AM+BM+CM=EN+MN+CM.
根据“两点之间线段最短”,得EN+MN+CM=EC最短
∴当M点位于BD与CE的交点处时,AM+BM+CM的值最小,即等于EC的长,
过E点作EF⊥BC交CB的延长线于F,
∴∠EBF=180°-120°=60°,
∵BC=2,
∴BF=1,EF=![]() ,在Rt△EFC中,
,在Rt△EFC中,
∵EF2+FC2=EC2,
EC=2![]() .
.
故答案为:2![]() .
.

 培优三好生系列答案
培优三好生系列答案【题目】某商场计划用3300元购进甲,乙两种商品共100个,这两种商品的进价、售价如下表:
进价(元/个) | 售价(元/个) | |
甲种 | 25 | 30 |
乙种 | 45 | 60 |
(1)求甲、乙两种商品各进多少个?
(2)全部售完100个商品后,该商场获利多少元?
【题目】某商场设立了一个可以自由旋转的转盘,并规定:顾客购物10元以上就能获得一次转动转盘的机会,当转盘停止时,指针落在哪一区域就可以获得相应的奖品.下表是活动进行中的一组落在奖品“铅笔”区域的统计数据:
转动转盘的次数 | 100 | 150 | 200 | 500 | 800 | 1000 |
落在“铅笔”的次数 | 68 | 111 | 136 | 345 | 564 | 701 |
落在“铅笔”的成功率 |
(1).计算并完成表格(精确到0.01);
(2).请估计,当![]() 很大时,落在“铅笔”区域的频率将会接近______(精确到0.1).
很大时,落在“铅笔”区域的频率将会接近______(精确到0.1).
(3).假如你去转动该转盘一次,你获得铅笔的成功率约是______.