题目内容
【题目】如图,已知二次函数![]() c为常数
c为常数![]() 的图象经过点
的图象经过点![]() ,点
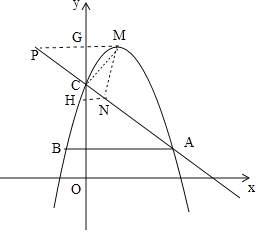
,点![]() ,顶点为点M,过点A作
,顶点为点M,过点A作![]() 轴,交y轴于点D,交该二次函数图象于点B,连结BC.
轴,交y轴于点D,交该二次函数图象于点B,连结BC.
![]() 求该二次函数的解析式及点M的坐标.
求该二次函数的解析式及点M的坐标.
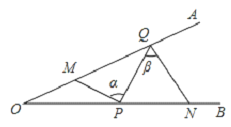
![]() 过该二次函数图象上一点P作y轴的平行线,交
过该二次函数图象上一点P作y轴的平行线,交![]() 一边于点Q,是否存在点P,使得以点P、Q、C、O为顶点的四边形为平行四边形,若存在,求出P点坐标;若不存在,说明理由.
一边于点Q,是否存在点P,使得以点P、Q、C、O为顶点的四边形为平行四边形,若存在,求出P点坐标;若不存在,说明理由.
![]() 点N是射线CA上的动点,若点M、C、N所构成的三角形与
点N是射线CA上的动点,若点M、C、N所构成的三角形与![]() 相似,请直接写出所有点N的坐标
相似,请直接写出所有点N的坐标![]() 直接写出结果,不必写解答过程
直接写出结果,不必写解答过程![]() .
.

【答案】![]() 二次函数解析式为
二次函数解析式为![]() ,点M的坐标为
,点M的坐标为![]() ;
;![]() 存在平行四边形,
存在平行四边形,![]() ;
;![]()
![]() ,
,![]() ,
,![]() ,
,![]() .
.
【解析】
![]() 将点A、点C的坐标代入函数解析式,即可求出b、c的值,通过配方法得到点M的坐标;
将点A、点C的坐标代入函数解析式,即可求出b、c的值,通过配方法得到点M的坐标;
![]() 根据平行四边形的判定对边平行且相等,可得关于m的方程,根据解方程,可得答案;
根据平行四边形的判定对边平行且相等,可得关于m的方程,根据解方程,可得答案;
![]() 由题意分析可得
由题意分析可得![]() ,则若
,则若![]() 与
与![]() 相似,则要进行分类讨论,分成
相似,则要进行分类讨论,分成![]() ∽
∽![]() 或
或![]() ∽
∽![]() 两种,然后利用边的对应比值求出N点坐标的横坐标,再利用自变量与函数值的对应关系,可得答案.
两种,然后利用边的对应比值求出N点坐标的横坐标,再利用自变量与函数值的对应关系,可得答案.
![]() 把点
把点![]() ,点
,点![]() 代入二次函数
代入二次函数![]() 得,
得,
![]() 解得
解得![]()
![]() 二次函数解析式为
二次函数解析式为![]() ,
,
配方得![]() ,
,
![]() 点M的坐标为
点M的坐标为![]() ;
;
![]() 由
由![]() 知,当
知,当![]() 时,
时,
![]() ,
,
解之,![]() 或
或![]()
![]()
![]() 、
、![]()
令P点横坐标为m,
![]() 当PQ与BC边相交时,
当PQ与BC边相交时,
![]() ,
,
![]() 此时不存在平行四边形.
此时不存在平行四边形.
![]() 当PQ与AC边相交时,
当PQ与AC边相交时,
由![]() 、
、![]() 可得直线AC解析式
可得直线AC解析式
![]() ,
,
![]() ,
,![]()
![]() ,
,
令![]()
![]() ,
,
![]() ,
,
![]() ,
,
此方程无解,
![]() 此时不存在平行四边形.
此时不存在平行四边形.
![]() 当PQ与AB边相交时,
当PQ与AB边相交时,
![]() 、
、![]()
![]() ,
,
令![]()
![]() ,
,
化简,得![]() ,
,
解得![]() ,
,
当![]() 时,
时,![]() ,
,
![]() 点坐标为
点坐标为![]() ,
,
此时,存在平行四边形,![]() ;
;
![]() 连接MC,作
连接MC,作![]() 轴并延长交AC于点N,则点G坐标为
轴并延长交AC于点N,则点G坐标为![]()
 ,
,
![]() ,
,![]()
![]() ,
,
把![]() 代入
代入![]() 解得
解得![]() ,则点P坐标为
,则点P坐标为![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
由此可知,若点N在AC上,则![]() ,则点D与点C必为相似三角形对应点
,则点D与点C必为相似三角形对应点
![]() 若有
若有![]() ∽
∽![]() ,则有
,则有![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
若点N在y轴右侧,作![]() 轴,
轴,
![]() ,
,![]()
![]() ,
,
把![]() 代入
代入![]() ,解得
,解得![]() ,
,
![]() ;
;
同理可得,若点N在y轴左侧,
把![]() 代入
代入![]() ,解得
,解得![]()
![]() ;
;
![]() 若有
若有![]() ∽
∽![]() ,则有
,则有![]()
![]() ,
,
![]() ,
,
若点N在y轴右侧,把![]() 代入
代入![]() ,解得
,解得![]() ;
;
若点N在y轴左侧,把![]() 代入
代入![]() ,解得
,解得![]()
![]() ;
;![]() .
.
![]() 所有符合题意得点N坐标有4个,分别为
所有符合题意得点N坐标有4个,分别为![]() ,
,![]() ,
,![]() ,
,![]() .
.