题目内容
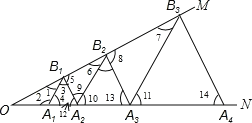
【题目】已知,∠MON=30°,点A1、A2、A3在射线ON上,点B1、B2、B3…在射线OM上,△A1B1A2、△A2B2A3、△A3B3A4…均为等边三角形,若OA1=a,则△A7B7A8的边长为______.

【答案】64a
【解析】
根据等腰三角形的性质以及平行线的性质得出A1B1∥A2B2∥A3B3,根据30°角所对直角边等于斜边的一半得到A2B2=2B1A2,进而得出A3B3=4B1A2=4a,A4B4=8B1A2=8a,A5B5=16B1A2…从而得到答案.
∵△A1B1A2是等边三角形,∴A1B1=A2B1,∠3=∠4=∠12=60°,∴∠2=120°.
∵∠MON=30°,∴∠1=180°﹣120°﹣30°=30°.
又∵∠3=60°,∴∠5=180°﹣60°﹣30°=90°.
∵∠MON=∠1=30°,∴OA1=A1B1=a,∴A2B1=a.
∵△A2B2A3、△A3B3A4是等边三角形,∴∠11=∠10=60°,∠13=60°.
∵∠4=∠12=60°,∴A1B1∥A2B2∥A3B3,B1A2∥B2A3,∴∠1=∠6=∠7=30°,∠5=∠8=90°,∴A2B2=2B1A2,B3A3=2B2A3,∴A3B3=4B1A2=4a,A4B4=8B1A2=8a,A5B5=16B1A2=16a,以此类推:A7B7=64B1A2=64a.
故答案为:64a.

【题目】某小学为每个班级配备了一种可以加热的饮水机,该饮水机的工作程序是:放满水后,接通电源,则自动开始加热,每分钟水温上升10℃,待加热到100℃,饮水机自动停止加热,水温开始下降,水温y(℃)和通电时间x(min)成反比例关系,直至水温降至室温,饮水机再次自动加热,重复上述过程.设某天水温和室温为20℃,接通电源后,水温和时间的关系如下图所示,回答下列问题:
(1)分别求出当0≤x≤8和8<x≤a时,y和x之间的关系式;
(2)求出图中a的值;
(3)下表是该小学的作息时间,若同学们希望在上午第一节下课8:20时能喝到不超过40℃的开水,已知第一节下课前无人接水,请直接写出生活委员应该在什么时间或时间段接通饮水机电源.(不可以用上课时间接通饮水机电源)
时间 | 节次 | |
上 午 | 7:20 | 到校 |
7:45~8:20 | 第一节 | |
8:30~9:05 | 第二节 | |
… | … | |







