Question

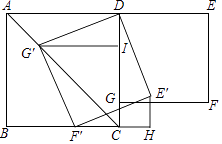
【题目】如图，将矩形沿直线折叠，顶点恰好落在边上点处，已知，则图中阴影部分面积为（ ）

A.B.C.D.

Answer 1

【答案】C

【解析】

根据折叠的性质求出DE＝EF＝5，在Rt△CEF中，利用勾股定理求出CF＝4，设AD＝x，则AD＝AF＝BC＝x，在Rt△ABF中，利用勾股定理构建方程即可解决问题．

解：设AD＝x，则AD＝AF＝BC＝x，

∵AB＝8，

∴CD＝AB＝8，

∵CE＝3，

∴EF＝DE＝CD﹣CE＝8﹣3＝5，

在直角△CEF中，CF＝＝4，

∴BF＝x﹣4，

在直角△ABF中，AB2+BF2＝AF2，即64+（x﹣4）2＝x2，

解得：x＝10，

∴S△ADE＝S△AFE＝ADDE＝×10×5＝25，

∵S矩形ABCD＝10×8＝80，

∴S阴影＝S矩形ABCD﹣S△ADE﹣S△AFE＝80﹣25﹣25＝30．

故选：C．