题目内容
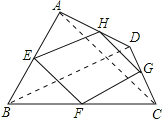
【题目】已知:如图,四边形ABCD四条边上的中点分别为E、F、G、H,顺次连接EF、FG、GH、HE,得到四边形EFGH(即四边形ABCD的中点四边形).
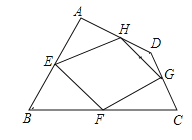
(1)四边形EFGH的形状是 ,证明你的结论.
(2)当四边形ABCD的对角线满足 条件时,四边形EFGH是矩形;
(3)你学过的哪种特殊四边形的中点四边形是矩形? .
【答案】(1)平行四边形,证明见解析.
(2)四边形ABCD的对角线满足互相垂直,证明见解析,
(3)菱形,证明见解析.
【解析】
(1)连接BD,根据三角形的中位线定理得到EH∥BD,EH=![]() BD,FG∥BD,FG═
BD,FG∥BD,FG═![]() BD,推出,EH∥FG,EH=FG,根据一组对边平行且相等的四边形是平行四边形得出四边形EFGH是平行四边形;
BD,推出,EH∥FG,EH=FG,根据一组对边平行且相等的四边形是平行四边形得出四边形EFGH是平行四边形;
(2)根据有一个角是直角的平行四边形是矩形,可知当四边形ABCD的对角线满足AC⊥BD的条件时,四边形EFGH是矩形;
(3)菱形的中点四边形是矩形.根据三角形的中位线平行于第三边并且等于第三边的一半可得四边形EFGH是平行四边形,再根据矩形的每一个角都是直角,然后根据平行线的性质,再根据垂直定义解答;
解:(1)四边形EFGH的形状是平行四边形.理由如下:
如图,连结BD. ∵E、H分别是AB、AD中点,
∴EH∥BD,EH= ![]() BD,
BD,
同理FG∥BD,FG=![]() BD,
BD,
∴EH∥FG,EH=FG,
∴四边形EFGH是平行四边形;
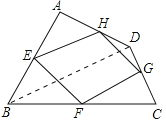
故答案为:平行四边形.
(2)当四边形ABCD的对角线满足互相垂直的条件时,四边形EFGH是矩形.
理由如下: 如图,连结AC、BD.
∵E、F、G、H分别为四边形ABCD四条边上的中点,
∴EH∥BD,HG∥AC,
∵AC⊥BD, ∴EH⊥HG,
又∵四边形EFGH是平行四边形,
∴平行四边形EFGH是矩形;
故答案为:对角线互相垂直.
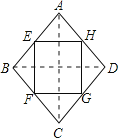
(3)菱形的中点四边形是矩形.
理由如下: 如图,连结AC、BD. ∵E、F、G、H分别为四边形ABCD四条边上的中点, ∴EH∥BD,HG∥AC,FG∥BD,EH=![]() BD,FG=
BD,FG=![]() BD,
BD,
∴EH∥FG,EH=FG,
∴四边形EFGH是平行四边形.
∵四边形ABCD是菱形,
∴AC⊥BD,
∵EH∥BD,HG∥AC,
∴EH⊥HG,
∴平行四边形EFGH是矩形;
故答案为:菱形.