题目内容
【题目】如图，抛物线y=﹣x2+2x+3与x轴交于A、B两点，与y轴交于C点，对称轴与抛物线相交于点M，与x轴相交于点N．点P是线段MN上的一动点，过点P作PE⊥CP交x轴于点E．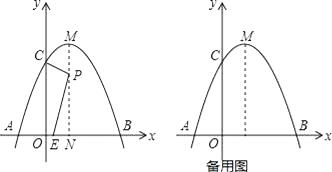
（1）直接写出抛物线的顶点M的坐标是 ．
（2）当点E与点O（原点）重合时，求点P的坐标．
（3）点P从M运动到N的过程中，求动点E的运动的路径长．
【答案】
（1）M（1，4）
（2）解：当点E与O重合时，EN=1，设PN=m，
过点C作CF⊥MN，垂足为F，如图1，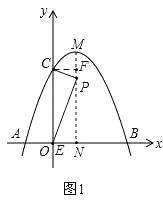
∵∠EPC=90°，
∴∠EPN+∠NEP=∠EPN+∠CPF=90°，
∴∠CPF=∠PEN，
∴△ENP∽△PFC
∴ 
，即： 
，
解得：m= 
∴点P的坐标为：（1， 
）或（1， 
）
（3）解：①当点P与M重合时，如图2，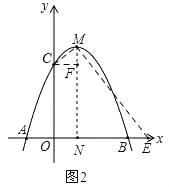
由△ENM∽△MFC可知， 
，
∴EN=4，
即当点P从M运动到F时，点E运动的路径长EN为4；
②当点P从F运动到N时，点E从点N向左运动到某最远点后，回到点N结束．如图3，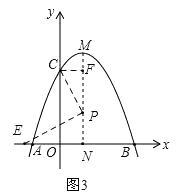
设EN=y，PN=x，
由△ENP∽△PFC可知， ，即： 
，
∴y= 
，
当x= 
时，y有最大值，为 
；
∴E的运动的路径长为： 
．
【解析】抛物线的顶点M的坐标是M（1，4）
练习册系列答案
相关题目
