题目内容
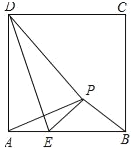
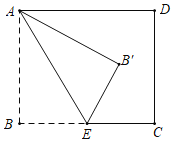
【题目】如图,在矩形ABCD中,已知AB=2,点E是BC边的中点,连接AE,△AB′E和△ABE关于AE所在直线对称,若△B′CD是直角三角形,则BC边的长为_____.
【答案】4或2![]()
【解析】
连接BB′,根据直角三角形的判定定理得到∠BB′C=90°,求得∠B′CD<90°,(1)如图1,∠B′DC=90°,(2)如图2,∠CB′D=90°,则B,B′D三点共线,设AE,BB′交于F,根据相似三角形的性质即可得到结论.
解:连接BB′,
∵BE=B′E=EC,
∴∠BB′C=90°,
∴∠B′CD<90°,
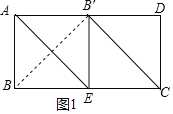
(1)如图1,∠B′DC=90°,
则四边形ABEB′和ECDB′是正方形,
∴BC=2AB=4,
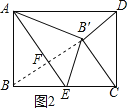
(2)如图2,∠CB′D=90°,
则B,B′D三点共线,
设AE,BB′交于F,
则F,B′是对角线BD的三等分点,
∵△BCB′∽△CDB′,
∴![]() ,
,
∴![]() ,
,
∴BC=![]() CD=2
CD=2![]() ,
,
故答案为:4或2![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目