Question

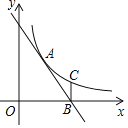
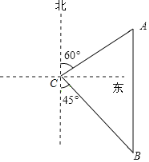
【题目】如图，一艘轮船从位于灯塔的北偏东60°方向，距离灯塔60海里的小岛出发，沿正南方向航行一段时间后，到达位于灯塔的南偏东45°方向上的处，这时轮船与小岛的距离是__________海里．

Answer 1

【答案】（30+30）

【解析】

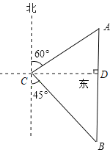
过点C作CD⊥AB，则在Rt△ACD中易得AD的长，再在Rt△BCD中求出BD，相加可得AB的长．

解：过C作CD⊥AB于D点，由题意可得，
∠ACD=30°，∠BCD=45°，AC=60．
在Rt△ACD中，cos∠ACD=,

∴AD=AC=30，CD=ACcos∠ACD=60×，

在Rt△DCB中，∵∠BCD=∠B=45°，
∴CD=BD=30，

∴AB=AD+BD=30+30．

答：此时轮船所在的B处与小岛A的距离是（30+30）海里．
故答案为：（30+30）．