题目内容
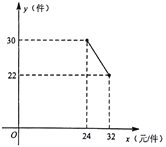
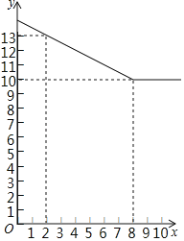
【题目】果农周大爷家的红心猕猴桃深受广大顾客的喜爱，猕猴桃成熟上市后，他记录了10天的销售数量和销售单价，其中销售单价y（元/千克）与时间第x天（x为整数）的数量关系如图所示，日销量P（千克）与时间第x天（x为整数）的部分对应值如表所示：
（1）请直接写出p与x的函数关系式及自变量x的取值范围；
（2）求y与x的函数关系式，并写出自变量x的取值范围；
（3）在这10天中，哪一天销售额达到最大，最大销售额是多少元．
【答案】（1）p=20x+200(0＜x≤10且x为整数)；（2）y=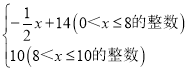
；（3）在这10天中，第10天销售额达到最大，最大销售额是4000元
【解析】
（1）从表格中的数据上看，是一次函数，用待定系数法可得p与x的函数关系式；
（2）是分段函数，利用待定系数法可得y与x的函数关系式；
（3）根据销售额=销量×销售单价，列函数关系式，并配方可得结论．
（1）由表格规律可知：p与x的函数关系是一次函数，
∴设解析式为：p=kx+b，
把(1，220)和(3，260)代入得：
，
∴
，
∴p=20x+200，
∴p与x的函数关系式为：p=20x+200(0＜x≤10且x为整数)
（2）①当0＜x≤8时，设y与x的解析式为：y=kx+b(k≠0)
把(2，13)和(8，10)代入得：
，
解得：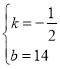
，
∴解析式为：y
x+14(k≠0)；
②当8＜x≤10时，y=10．
综上所述：y与x(x为整数)的函数关系式为：y
；
（3）设销售额为w元，
当0＜x≤8时，w=py=(
x+14)(20x+200)=﹣10x2+180x+2800=﹣10(x﹣9)2+3610．
∵x是整数且0＜x≤8，
∴当x=8时，w有最大值为：﹣10(8﹣9)2+3610=3600，
当8＜x≤10时，w=py=10(20x+200)=200x+2000．
∵x是整数，200＞0，
∴当8＜x≤10时，w随x的增大而增大，
∴当x=10时，w有最大值为：200×10+2000=4000．
∵3600＜4000，
∴在这10天中，第10天销售额达到最大，最大销售额是4000元．
