题目内容
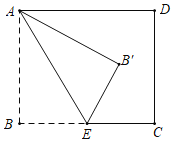
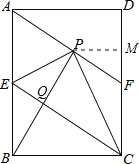
【题目】如图,在矩形ABCD中,E是AB边的中点,沿EC对折矩形ABCD,使B点落在点P处,折痕为EC,连结AP并延长AP交CD于F点,
(1)求证:△CBE≌△CPE;
(2)求证:四边形AECF为平行四边形;
(3)若矩形ABCD的边AB=6,BC=4,求△CPF的面积.

【答案】(1)见解析;(2)见解析;(3)![]()
【解析】
(1)由折叠的性质可知:EP=EB,CP=CE,根据SSS证明三角形全等即可;
(2)由折叠的性质得到BE=PE,EC与PB垂直,根据E为AB中点,得到AE=EB=PE,利用一边上的中线等于这条边的一半的三角形为直角三角形,得到∠APB为90°,进而得到AF与EC平行,再由AE与FC平行,利用两对边平行的四边形为平行四边形即可得证;
(3)过P作PM⊥CD,在直角三角形EBC中,利用勾股定理求出EC的长,利用面积法求出BQ的长,根据BP=2BQ求出BP的长,在直角三角形ABP中,利用勾股定理求出AP的长,根据AF﹣AP求出PF的长,由PM与AD平行,得到三角形PMF与三角形ADF相似,由相似得比例求出PM的长,再由FC=AE=3,求出三角形CPF面积即可.
(1)解:由折叠可知,EP=EB,CP=CB,
∵EC=EC,
∴△ECP≌△ECB(SSS).
(2)证明:由折叠得到BE=PE,EC⊥PB,
∵E为AB的中点,
∴AE=EB=PE,
∴AP⊥BP,
∴AF∥EC,
∵AE∥FC,
∴四边形AECF为平行四边形;
(3)过P作PM⊥DC,交DC于点M,
在Rt△EBC中,EB=3,BC=4,
根据勾股定理得:![]()
![]() ,
,
![]() ,
,
由折叠得:BP=2BQ=![]() ,
,
在Rt△ABP中,AB=6,BP=![]() ,
,
根据勾股定理得: 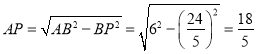 ,
,
∵四边形AECF为平行四边形,
∴AF=EC=5,FC=AE=3,
∴PF=5﹣![]() =
=![]() ,
,
∵PM∥AD,
∴△FPM∽△FAD
![]() ,即
,即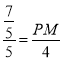
解得:PM=![]() ,
,
则S△PFC=![]() FCPM=
FCPM=![]() ×3×
×3×![]() =
=![]() .
.

【题目】某校门口竖着“前方学校,减速慢行”的交通指示牌CD,数学“综合与实践”小组的同学将“测量交通指示牌CD的高度”作为一项课题活动,他们定好了如下测量方案:
项目 | 内容 |
课题 | 测量交通指示牌CD的高度 |
测量示意图 |
|
测量步骤 | (1)从交通指示牌下的点M处出发向前走10 米到达A处; (2)在点A处用量角仪测得∠DAM=27°; (3)从点A沿直线MA向前走10米到达B处;(4)在点B处用量角仪测得∠CBA=18°. |
请你帮助该小组同学根据上表中的测量数据,求出交通指示牌CD的高度.(参考数据sin27°≈0.45,cos27°≈0.89,tan27°≈0.51,sin18°≈0.31,cos18°≈0.95,tan18°≈0.32)
【题目】某商场同时购进甲、乙两种商品共100件,其进价和售价如下表:
商品名称 | 甲 | 乙 |
进价(元/件) | 40 | 90 |
售价(元/件) | 60 | 120 |
设其中甲种商品购进x件,商场售完这100件商品的总利润为y元.
(Ⅰ)写出y关于x的函数关系式;
(Ⅱ)该商场计划最多投入8000元用于购买这两种商品,
①至少要购进多少件甲商品?
②若销售完这些商品,则商场可获得的最大利润是多少元?