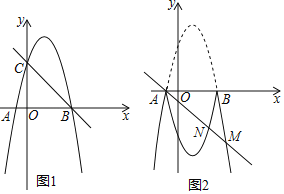
题目内容
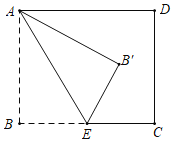
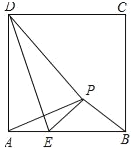
【题目】如图,正方形ABCD中,AD=![]() +2,已知点E是边AB上的一动点(不与A、B重合)将△ADE沿DE对折,点A的对应点为P,当△APB是等腰三角形时,AE=_____.
+2,已知点E是边AB上的一动点(不与A、B重合)将△ADE沿DE对折,点A的对应点为P,当△APB是等腰三角形时,AE=_____.
【答案】1或![]()
【解析】
分两种情况讨论:若AP=BP时,△ADP是等边三角形;若AP=AB时,点P在AB的垂直平分线上,且PF⊥AD,得到PF=![]() AB,在理折叠的性质和正方形性质即可解答
AB,在理折叠的性质和正方形性质即可解答
若AP=BP,
∵四边形ABCD是正方形
∴AD=AB,∠DAB=90°,
∵折叠
∴AD=DP=AP,∠ADE=∠PDE
∴△ADP是等边三角形
∴∠ADP=60°
∴∠ADE=30°
∴AE=![]() =
=![]()
若AP=AB,
如图,过点P作PF⊥AD于点F,作∠MED=∠MDE,
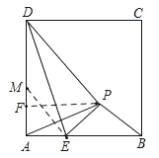
∵AP=PB,
∴点P在AB的垂直平分线上,且PF⊥AD,
∴PF=![]() AB,
AB,
∵折叠
∴AD=DP=AB,∠ADE=∠PDE
∴PF=![]() PD
PD
∴∠PDF=30°
∴∠ADE=15°
∵∠MED=∠MDE,
∴∠AME=30°,ME=MD
∴AM=![]() AE,ME=2AE
AE,ME=2AE
∴AD=2AE+![]() AE=2+
AE=2+![]()
∴AE=1
故答案为1或 ![]()

练习册系列答案
相关题目