题目内容
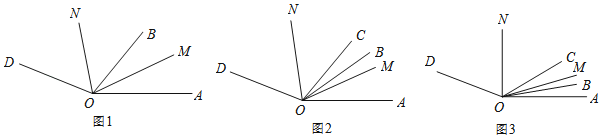
【题目】(1)如图1,已知∠AOB=90°,∠BOC=30°,OM平分∠AOC,ON平分∠BOC.填空:∠MON= ;
(2)如图2,∠AOB=90°,∠BOC=x ,仍然分别作∠AOC、∠BOC的平分线OM、ON,能否求出∠MON的度数?若能,求出其值;若不能,说明理由.
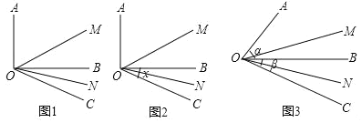
(3)如图3,若∠AOB=α,∠BOC=β(α、β均为锐角,且α>β),仍然分别作∠AOC、∠BOC的平分线OM、ON,能否求出∠MON的度数.若能,求∠MON的度数.
(4)从(1)、(2)、(3)的结果中,你发现了什么规律?
【答案】(1)45°;(2)能,![]() ;(3)能,
;(3)能,![]() ;(4)
;(4)![]()
【解析】
(1)根据题意可知,∠AOC=120°,由OM平分∠AOC,ON平分∠BOC;推出∠MOC=∠AOC=60°,∠CON= ![]() ∠BOC=15°,由图形可知,∠MON=∠MOC-∠CON,即可求出∠MON=45°;
∠BOC=15°,由图形可知,∠MON=∠MOC-∠CON,即可求出∠MON=45°;
(2)根据(1)的求解思路,先利用角平分线的定义表示出∠MOC与∠NOC的度数,然后相减即可得到∠MON的度数;
(3)用α、β表示∠MOC,∠NOC,根据∠MON=∠MOC-∠NOC得解.
(4)由(1)、(2)、(3)的结果中,∠MON的度数与∠BCO无关,∠MON= ![]() .
.
(1)∵∠AOB=90°,∠BOC=30°,
∴∠AOC=∠AOB+∠BOC=90°+30°=120°,
∵OM平分∠AOC,ON平分∠BOC,
∴∠MOC=∠AOC=60°,∠CON= ![]() ∠BOC=15°,
∠BOC=15°,
∴∠MON=∠MOC-∠CON=60°-15°=45°;
(2)能.
∵∠AOB=90°,∠BOC=x,
∴∠AOC=90°+x,
∵OM、ON分别平分∠AOC,∠BOC,
∴∠MOC= ![]() ∠AOC=
∠AOC= ![]() (90°+x°)=45°+
(90°+x°)=45°+ ![]() x,
x,
∴∠CON= ![]() ∠BOC=
∠BOC= ![]() x,
x,
∴∠MON=∠MOC-∠CON=45°+ ![]() x-
x- ![]() x=45°.
x=45°.
(3)∵∠AOB=α,∠BOC=β,
∴∠AOC=∠AOB+∠BOC=α+β,
∵OM平分∠AOC,
∴∠MOC= ![]() ∠AOC=
∠AOC= ![]() (α+β),
(α+β),
∵ON平分∠BOC,
∴∠NOC= ![]() ∠BOC=
∠BOC= ![]() ,
,
∴∠MON=∠MOC-∠NOC= ![]() (α+β)-
(α+β)-![]() =
=![]() .
.
(4)规律:∠MON的度数与∠BCO无关,∠MON=![]() .理由如下:
.理由如下:
∵∠AOB=α,∠BOC=β,
∴∠AOC=∠AOB+∠BOC=α+β,
∵OM平分∠AOC,
∴∠MOC=![]() ∠AOC=
∠AOC=![]() (α+β),
(α+β),
∵ON平分∠BOC,
∴∠NOC=![]() ∠BOC=
∠BOC=![]() ,
,
∴∠MON=∠MOC-∠NOC=![]() (α+β)-
(α+β)-![]() =
=![]() .
.