Question

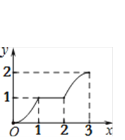
【题目】在一个不透明的盒子里装有颜色不同的黑、白两种球共40个,小颖做摸球试验,她将盒子里面的球搅匀后从中随机摸出一个球记下颜色,再把它放回盒子中,不断重复上述过程,下表是“摸到白色球”的频率折线统计图.

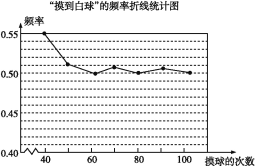
(1)请估计:当n足够大时,摸到白球的频率将会稳定在　　　　　　(精确到0.01),假如你摸一次,你摸到白球的概率为　　　　　　;

(2)试估算盒子里白、黑两种颜色的球各有多少个?

(3)在(2)条件下如果要使摸到白球的概率为,需要往盒子里再放入多少个白球?

Answer 1

【答案】（1）0.5，0.5；（2）两种颜色的球各有20个；（3）10个.

【解析】

（1）根据所给“频率折线图”进行分析判断即可；

（2）根据（1）中所得概率进行计算即可；

（3）设需再放入x个白球，结合（2）中结果列出方程，解此方程即可得到所求答案.

(1)根据题意可得：当n足够大时，摸到白球的概率会接近0.50；假如你摸一次，你摸到白球的概率为0.5；

(2)∵40×0.5=20，40-20=20，

∴盒子里白、黑两种颜色的球各有20个；

(3)设需要往盒子里再放入x个白球，根据题意得：

，

解得x=10，

经检验，x=10是所列方程的根，

故需要往盒子里再放入10个白球.