题目内容
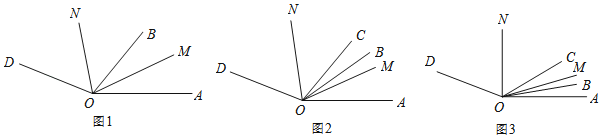
【题目】已知:∠AOD=150°,OB,OM,ON是∠AOD内的射线.
(1)如图1,若OM平分∠AOB,ON平分∠BOD.当射线OB绕点O在∠AOD内旋转时,
∠MON= °;
(2)OC也是∠AOD内的射线,如图2,若∠BOC=m°,OM平分∠AOC,ON平分∠BOD,
求∠MON的大小(用含m的式子表示);
(3)在(2)的条件下,若m=20,∠AOB=10°,当∠BOC在∠AOD内部绕O点以每秒2°的速度逆时针旋转t秒,如图3,若3∠AOM=2∠DON时,求t的值.
【答案】(1)75;(2)(75-![]() m)°;(3)t为19秒.
m)°;(3)t为19秒.
【解析】
(1)根据角平分线的定义,以及角度和的关系,可得∠MON=![]() ∠AOD即可得出;
∠AOD即可得出;
(2)根据角平分线的定义,得出∠MOC=![]() ∠AOC,∠BON=
∠AOC,∠BON=![]() ∠BOD,利用角度和与差的关系,得出∠MON=∠MOC+∠BON﹣∠BOC,角度代换即可得出结果;
∠BOD,利用角度和与差的关系,得出∠MON=∠MOC+∠BON﹣∠BOC,角度代换即可得出结果;
(3)由题意知,∠AOM=![]() (10+2t+20°),∠DON=
(10+2t+20°),∠DON=![]() (150﹣10﹣2t)°,根据3∠AOM=2∠DON,列出方程求解即可.
(150﹣10﹣2t)°,根据3∠AOM=2∠DON,列出方程求解即可.
解:(1)∵OM平分∠AOB,ON平分∠BOD,
∴∠MOB=![]() ∠AOB,∠BON=
∠AOB,∠BON=![]() ∠BOD,
∠BOD,
∴∠MON=∠MOB+∠BON,
=![]() ∠AOB+
∠AOB+![]() ∠BOD,
∠BOD,
=![]() ∠AOD,
∠AOD,
=![]() ×150°,
×150°,
=75°,
故答案为:75;
(2)∵OM平分∠AOC,ON平分∠BOD,
∴∠MOC=![]() ∠AOC,∠BON=
∠AOC,∠BON=![]() ∠BOD,
∠BOD,
∠MON=∠MOC+∠BON﹣∠BOC
=![]() ∠AOC+
∠AOC+![]() ∠BOD﹣∠BOC
∠BOD﹣∠BOC
=![]() (∠AOC+∠BOD)﹣∠BOC
(∠AOC+∠BOD)﹣∠BOC
=![]() (∠AOB+∠BOC+∠BOD)﹣∠BOC
(∠AOB+∠BOC+∠BOD)﹣∠BOC
=![]() (∠AOD+∠BOC)﹣∠BOC
(∠AOD+∠BOC)﹣∠BOC
=![]() ×(150°+m°)﹣m°
×(150°+m°)﹣m°
=(75-![]() m)°,
m)°,
故答案为:(75-![]() m)°;
m)°;
(3)∵∠AOM=![]() ∠AOC=
∠AOC=![]() (10+2t+20°)=(15+t)°,
(10+2t+20°)=(15+t)°,
∠DON=![]() ∠BOD=
∠BOD=![]() (150﹣10﹣2t)°=(70-t)°,
(150﹣10﹣2t)°=(70-t)°,
又∵3∠AOM=2∠DON,
∴3(15+t)=2(70﹣t),
得t=19.
答:t为19秒,
故答案为:19秒.

【题目】列方程组解应用题某校组织“大手拉小手,义卖献爱心”活动,计划购买黑、白两种颜色的文化衫进行手绘设计后出售,并将所获利润全部捐给山区困难孩子.已知该学校从批发市场花2400元购买了黑、白两种颜色的文化衫100件,每件文化衫的批发价及手绘后的零售价如表:
批发价(元) | 零售价(元) | |
黑色文化衫 | 25 | 45 |
白色文化衫 | 20 | 35 |
(1)学校购进黑、白文化衫各几件?
(2)通过手绘设计后全部售出,求该校这次义卖活动所获利润.