题目内容
问题1:如图1,在四边形ABCD中,AD∥BC,∠A=∠D,AB=BC=CD,点M,N分别在AD,CD上,若∠MBN= ∠ABC,试探究线段MN,AM,CN有怎样的数量关系?请直接写出你的猜想,不用证明;
∠ABC,试探究线段MN,AM,CN有怎样的数量关系?请直接写出你的猜想,不用证明;
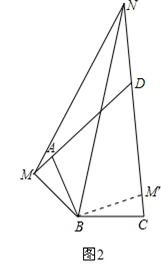
问题2:如图2,在四边形ABCD中,AB=BC,∠ABC+∠ADC=180°,点M,N分别在DA,CD的延长线上,若∠MBN= ∠ABC仍然成立,请你进一步探究线段MN,AM,CN又有怎样的数量关系?写出你的猜想,并给予证明.
∠ABC仍然成立,请你进一步探究线段MN,AM,CN又有怎样的数量关系?写出你的猜想,并给予证明.

解:(1)猜想:____________________
(2)猜想:____________________
证明:
 ∠ABC,试探究线段MN,AM,CN有怎样的数量关系?请直接写出你的猜想,不用证明;
∠ABC,试探究线段MN,AM,CN有怎样的数量关系?请直接写出你的猜想,不用证明;问题2:如图2,在四边形ABCD中,AB=BC,∠ABC+∠ADC=180°,点M,N分别在DA,CD的延长线上,若∠MBN=
 ∠ABC仍然成立,请你进一步探究线段MN,AM,CN又有怎样的数量关系?写出你的猜想,并给予证明.
∠ABC仍然成立,请你进一步探究线段MN,AM,CN又有怎样的数量关系?写出你的猜想,并给予证明. 
解:(1)猜想:____________________
(2)猜想:____________________
证明:
(1)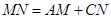 ;(2)
;(2) .
.
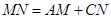 ;(2)
;(2) .
.试题分析:(1)如图1,先判定梯形
 是等腰梯形,根据等腰梯形的性质可得
是等腰梯形,根据等腰梯形的性质可得 ,再把
,再把 绕点
绕点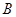 顺时针旋转使点
顺时针旋转使点 与点
与点 重合,点
重合,点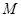 到达点
到达点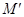 ,根据旋转变换的性质,
,根据旋转变换的性质, 和
和 全等,根据全等三角形对应边相等可得
全等,根据全等三角形对应边相等可得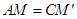 ,
, ,根据全等三角形对应角相等可得
,根据全等三角形对应角相等可得 ,
,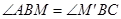 ,然后证明
,然后证明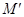 、
、 、
、 三点共线,再利用“边角边”证明
三点共线,再利用“边角边”证明 和
和 全等,然后根据全等三角形对应边相等即可得证.
全等,然后根据全等三角形对应边相等即可得证.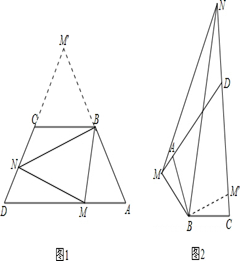
(2)如图2,在
 内部作
内部作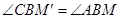 交
交 于点
于点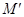 ,然后证明
,然后证明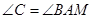 ,再利用“角边角”证明
,再利用“角边角”证明 和
和 全等,根据全等三角形对应边相等可得
全等,根据全等三角形对应边相等可得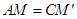 ,
, ,再证明
,再证明 ,利用“边角边”证明
,利用“边角边”证明 和
和 全等,根据全等三角形对应边相等可得
全等,根据全等三角形对应边相等可得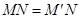 ,从而得到
,从而得到 .
.
试题解析:解:猜想的结论:(1)
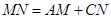 ;(2)猜想的结论:
;(2)猜想的结论: .
.理由如下:如图,作
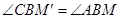 交
交 于点
于点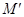 ,
,∵
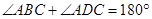 ,
,∴
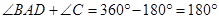 ,
,又∵
 ,
,∴
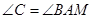 ,
,在
 和
和 中,
中, ,
,∴
 ,
,∴
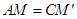 ,
, ,
,∵
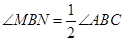 ,
,∴
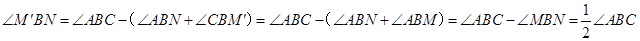 ,
,∴
 ,
,在
 和
和 中,
中,∵
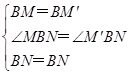 ,
,∴
 ,
,∴
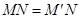 ,
,∵
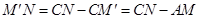 ,
,∴
 .
.
练习册系列答案
相关题目
 中,
中, ,
, .点
.点 ,
, ,
,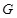 分别在边
分别在边 ,
, ,
, 上,
上, .
.
 是平行四边形;
是平行四边形; 时,求证:四边形
时,求证:四边形



 cm2 B.
cm2 B. cm2 C.
cm2 C. cm2 D.
cm2 D. cm2
cm2