Question

【题目】如图，AB是半圆O的直径，C是半圆O上一点（不与点A、B重合），D是的中点，DE⊥AB于点E，过点C作半圆O的切线，交ED的延长线于点F．

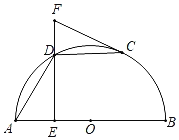
（1）求证：∠FCD＝∠ADE；

（2）填空：

①当∠FCD的度数为　 　时，四边形OADC是菱形；

②若AB＝2，当CF∥AB时，DF的长为　 　．

Answer 1

【答案】（1）见解析；（2）①30°；②﹣1．

【解析】

（1）如下图，先推导出∠OAD＝∠OCD，然后再利用CF⊥OC和DE⊥AB进行角度转化，推导出∠FCD＝∠ADE；

（2）①当∠FCD=30°时，可得到△OAD是等边三角形，然后再推导出△COD也是等边三角形，从而证菱形；

②如下图，先证△ADE≌△DCF，得出AE＝DF，DE＝CF，推导出△ODE是等腰直角三角形，从而求出DF的长．

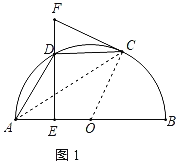
（1）证明：连接OC、AC．如图1所示：

∵D是的中点，

∴＝，

∴DA＝DC，

∴∠DAC＝∠DCA．

∵OA＝OC，

∴∠OAC＝∠OCA．

∴∠DAC+∠OAC＝∠DCA+∠OCA，

即∠OAD＝∠OCD．

∵CF是半圆O的切线，

∴CF⊥OC，

∴∠FCD+∠OCD＝90°，

∵DE⊥AB，

∴∠ADE+∠OAD＝90°，

∴∠FCD＝∠ADE．

（2）解：①当∠FCD的度数为30°时，四边形OADC是菱形；理由如下：

连接OD，如图2所示：

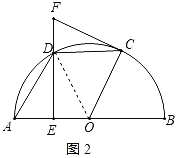
∵∠FCD＝30°，

∴∠ADE＝30°，

∵DE⊥AB，

∴∠OAD＝60°，

∵OA＝OD，

∴△OAD是等边三角形，

∴AD＝OA，∠AOD＝60°，

∵D是的中点，

∴＝，

∴∠AOD＝∠COD＝60°，

∵OC＝OD，

∴△COD是等边三角形，

∴CD＝OD＝OC，

∴OA＝AD＝CD＝OC，

∴四边形OADC是菱形；

故答案为：30°；

②连接OD，如图3所示：

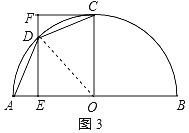
∵AB＝2，

∴OA＝OD＝，

∵CF∥AB，DE⊥AB，

∴CF⊥EF，

∴∠CFD＝90°＝∠DEA，

在△ADE和△DCF中，，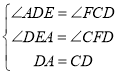

∴△ADE≌△DCF（AAS），

∴AE＝DF，DE＝CF，

∵CF半圆O的切线，

∴CF⊥OC，

∴四边形OCFE是矩形，

∴CF＝OE，

∴DE＝OE，

∴△ODE是等腰直角三角形，

∴OE＝OD＝1，

∴DF＝AE＝OA﹣OE＝﹣1；

故答案为：﹣1．