��Ŀ����
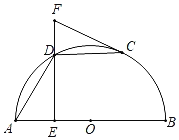
����Ŀ����֪������y����![]() x2+bx+c������A��4��3��������ΪB���Գ�����ֱ��x��2��
x2+bx+c������A��4��3��������ΪB���Գ�����ֱ��x��2��
��1���������ߵĺ�������ʽ�Ͷ���B�����ꣻ
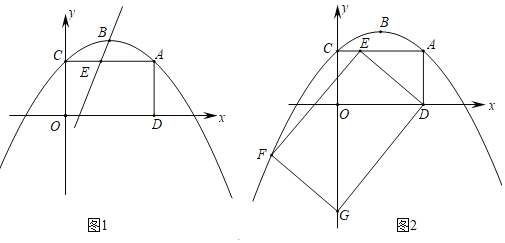
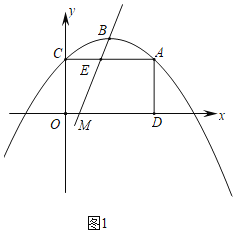
��2����ͼ1����������y�ύ�ڵ�C������AC����A��AD��x���ڵ�D��E���߶�AC�ϵĶ��㣨��E����A��C�����غϣ���
��i����ֱ��BE���ı���ACOD�ֳ������Ϊ1��3�������֣����E�����ꣻ
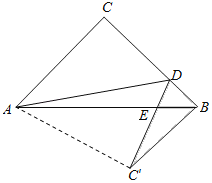
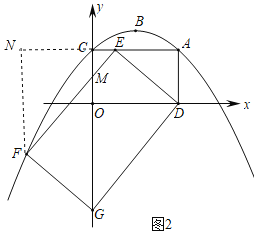
��ii����ͼ2������DE��������DEFG���ڵ�E���˶������У��Ƿ���ڵ�G����y���ϵ�ͬʱ��Fǡ�������������ϣ������ڣ������ʱAE�ij����������ڣ���˵�����ɣ�
���𰸡���1��y����![]() x2+x+3������B������Ϊ��2��4������2����i����E������Ϊ��
x2+x+3������B��������2��4������2����i����E��������![]() ��3����
��3����![]() ��3������ii�����ڣ�����G����y���ϵ�ͬʱ��Fǡ�������������ϣ���ʱAE�ij�Ϊ
��3������ii�����ڣ�����G����y���ϵ�ͬʱ��Fǡ�������������ϣ���ʱAE�ij�Ϊ![]() ��
��
��������
��1��������ó�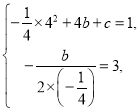 �����
�����![]() ���ó������ߵĺ�������ʽΪ��y����
���ó������ߵĺ�������ʽΪ��y����![]() x2+x+3����
x2+x+3����![]() ��x��2��2+4�����ɵó�����B������Ϊ��2��4����
��x��2��2+4�����ɵó�����B������Ϊ��2��4����
��2����i�����C��0��3�������E������Ϊ��m��3�������ֱ��BE�ĺ�������ʽΪ��y��![]() x+
x+![]() �����M������Ϊ��4m��6��0����������ó�OC��3��AC��4��OM��4m��6��CE��m����S����ACOD��12��S����ECOM��
�����M������Ϊ��4m��6��0����������ó�OC��3��AC��4��OM��4m��6��CE��m����S����ACOD��12��S����ECOM��![]() ��������������m��ֵ���ɣ�
��������������m��ֵ���ɣ�
��ii������F��FN��AC��N����NF��CG�����F����������a����![]() a2+a+3������NF��3������
a2+a+3������NF��3������![]() a2+a+3����
a2+a+3����![]() a2��a��NC����a��֤��EFN�ա�DGO��ASA�����ó�NE��OD��AC��4����AE��NC����a��֤��ENF�ס�DAE���ó�
a2��a��NC����a��֤��EFN�ա�DGO��ASA�����ó�NE��OD��AC��4����AE��NC����a��֤��ENF�ס�DAE���ó�![]() �����a����
�����a����![]() ��0����a��0ʱ����E���A�غϣ���ȥ���ó�AE��NC����a��
��0����a��0ʱ����E���A�غϣ���ȥ���ó�AE��NC����a��![]() �����ɵó����ۣ�
�����ɵó����ۣ�
��1����������y����![]() x2+bx+c������A��4��3�����Գ�����ֱ��x��2��
x2+bx+c������A��4��3�����Գ�����ֱ��x��2��
��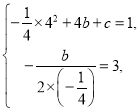
���![]()
�������ߵĺ�������ʽΪ��y����![]() x2+x+3��
x2+x+3��
��y����![]() x2+x+3����
x2+x+3����![]() ��x��2��2+4��
��x��2��2+4��
�ඥ��B������Ϊ��2��4����
��2����i����y����![]() x2+x+3��
x2+x+3��
��x��0ʱ��y��3��
��C���������0��3����
��A��4��3����
��AC��OD��
��AD��x��
���ı���ACOD�Ǿ��Σ�
���E������Ϊ��m��3����ֱ��BE�ĺ�������ʽΪ��y��kx+n��ֱ��BE��x���ڵ�M����ͼ1��ʾ��
��![]()
��ã� 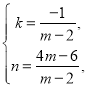 ��
��
��ֱ��BE�ĺ�������ʽΪ��y��![]() x+
x+![]() ��
��
�y��![]() x+
x+![]() ��0����x��4m��6��
��0����x��4m��6��
���M��������4m��6��0����
��ֱ��BE���ı���ACOD�ֳ������Ϊ1��3�������֣�
���M���߶�OD�ϣ���M�����O�غϣ�
��C��0��3����A��4��3����M��4m��6��0����E��m��3����
��OC��3��AC��4��OM��4m��6��CE��m��
��S����ACOD��OCAC��3��4��12��
S����ECOM��![]() ��OM+EC��OC��
��OM+EC��OC��![]() ��4m��6+m����3��
��4m��6+m����3��![]() ��
��
�����������
��![]() ��
��![]() ����
����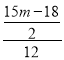 ��
��![]() ��
��
��ã�m��![]() ��
��
���E����������![]() ��3����
��3����
��![]() ��
��![]() ����
����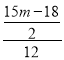 ��
��![]() ��
��
��ã�m��![]() ��
��
���E����������![]() ��3����
��3����
������������E����������![]() ��3����
��3����![]() ��3����
��3����
��ii�����ڵ�G����y���ϵ�ͬʱ��Fǡ�������������ϣ��������£�
������ã����������ľ���DEFG��ֱ��AC���·���
����F��FN��AC��N����NF��CG����ͼ2��ʾ��
���F����������a����![]() a2+a+3����
a2+a+3����
��NF��3������![]() a2+a+3����
a2+a+3����![]() a2��a��NC����a��
a2��a��NC����a��
���ı���DEFG���ı���ACOD���Ǿ��Σ�
���DAE����DEF����N��90�㣬EF��DG��EF��DG��AC��OD��
���NEF����ODG����EMC����DGO��
��NF��CG��
���EMC����EFN��
���EFN����DGO��
�ڡ�EFN�͡�DGO�У���NEF=��ODG��EF=DG,��EFN=��DGO��
���EFN�ա�DGO��ASA����
��NE��/span>OD��AC��4��
��AC��CE��NE��CE����AE��NC����a��
�ߡ�DAE����DEF����N��90�㣬
���NEF+��EFN��90�㣬��NEF+��DEA��90�㣬
���EFN����DEA��
���ENF�ס�DAE��
��![]() ����
����![]() ��
��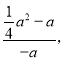
�����ã�![]() a2+a��0��
a2+a��0��
��ã�a����![]() ��0��
��0��
��a��0ʱ����E���A�غϣ�
��a��0��ȥ��
��AE��NC����a��![]() ��
��
�൱��G����y���ϵ�ͬʱ��Fǡ�������������ϣ���ʱAE�ij�Ϊ![]() ��
��

 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�