Question

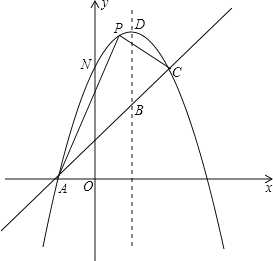
【题目】如图，直线y＝﹣2x+c交x轴于点A（3，0），交y轴于点B，抛物线y＝﹣x2+bx+c经过点A，B．

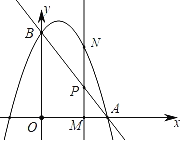
（1）求抛物线的解析式；

（2）点M（m，0）是线段OA上一动点（点M不与点O，A重合），过点M作y轴的平行线，交直线AB于点P，交抛物线于点N，若NP＝AP，求m的值；

（3）若抛物线上存在点Q，使∠QBA＝45°，请直接写出相应的点Q的坐标．

Answer 1

【答案】（1）y＝﹣x2+x+6；（2）m＝；（3）点Q的坐标为（，）或（﹣2，0）．

【解析】

（1）将点A、B代入函数解析式，可求得b、c的值；

（2）利用△APM∽△ABO，可取得AP的值，然后再根据NP＝AP，可求出m的值；

（3）存在2种情况，一种是点Q在AB的上方，另一种是点Q在AB的下方，分别利用几何性质计算可求得．

（1）∵y＝﹣2x+c与x轴交于点A(3，0)，与y轴交于点B，

∴﹣2×3+c＝0，解得c＝6，

∴B(0，6)，

∵抛物线y＝﹣x2+bx+c经过点A，B，

∴，解得，

∴抛物线解析式为y＝﹣x2+x+6．

（2）由点M（m，0），得点P(m，﹣2m+6)，点N(m，﹣m2+m+6)，

∴NP＝﹣m2+3m．

在Rt△OAB中，AB＝＝3，

∵MP∥y轴，

∴△APM∽△ABO，

∴，即，

∴AP＝(3﹣m)，

∵NP＝AP，

∴﹣m2+3m＝×(3﹣m)，解得：m＝或3(舍去3)，

∴m＝．

（3）点Q的坐标为(，或(﹣2，0)．

①当点Q在AB上方时，

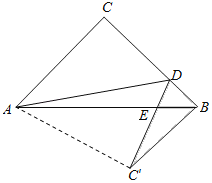
设点Q的横坐标为n，如图，分别作QC⊥AB，QD⊥x轴，交AB于点E．

则点E(n，﹣2n+6)，点Q(n，﹣n2+n+6)，

则QE＝﹣n2+n+6﹣(﹣2n+6)＝﹣n2+3n，

∵∠CQE＝90°﹣∠QEC＝90°﹣∠AED＝∠EAD，

∴Rt△QEC∽Rt△ABO，

，

则QC＝，CE＝，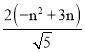

∵∠QBA＝45°，

∴BC＝QC＝，

∵ED∥OB，

∴，即，解得：BE＝n，

而BE＝BC+CE，

∴+＝n，解得n＝，

∴点Q的坐标为(，)；

②当点Q在AB下方时，

同理可求，另一点Q的坐标为(﹣2，0)，

故点Q的坐标为(，)或(﹣2，0)．