题目内容
如图,已知在△ABC中,∠ACB=90°,点D、E、F分别是AC、AB、BC的中点,
试说明:CE=DF.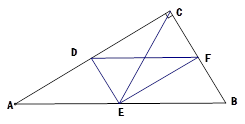
试说明:CE=DF.

先根据三角形的中位线定理可得四边形CDEF为平行四边形,再结合∠ACB=90°可证得平行四边形CDEF为矩形,从而证得结论.
试题分析:∵点D、E、F分别是AC、AB、BC的中点
∴DE∥CF,CD∥EF
∴四边形CDEF为平行四边形
∵∠ACB=90°
∴平行四边形CDEF为矩形
∴CE=DF.
点评:解答本题的关键是熟练掌握三角形的中位线定理:三角形的中位线平行于第三边,且等于第三边的一半.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目


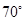 ,则其底角为 .
,则其底角为 .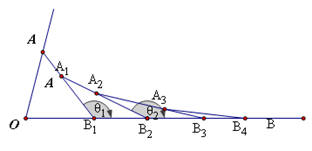


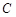 是
是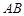 的中点,
的中点,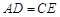 ,
,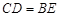 .求证:△
.求证:△ ≌△
≌△ .
.

 、G9,,若∠BDC=1400,∠BG1C=77°,求∠A的度数。
、G9,,若∠BDC=1400,∠BG1C=77°,求∠A的度数。