题目内容
(12分)如图⑴所示的图形,像我们常见的学习用品——圆规。我们不妨把这样图形叫做“规形图”,那么在这一个简单的图形中,到底隐藏了哪些数学知识呢?下面就请你发挥你的聪明才智,解决以下问题:
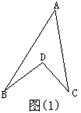

⑴观察“规形图”,试探究∠BDC与∠A、∠B、∠C之间的关系,并说明理由;
⑵请你直接利用以上结论,解决以下三个问题:
①如图(2),把一块三角尺XYZ放置在△ABC上,使三角尺的两条直角边XY、XZ恰好经过点B、C,若∠A=50°,则∠ABX+∠ACX =__________°;
②如图(3),DC平分∠ADB, EC平分∠AEB,若∠DAE=50°,∠DBE=130°,求∠DCE的度数;
③如图(4),∠ABD,∠ACD的10等分线相交于点G1、G2 、G9,,若∠BDC=1400,∠BG1C=77°,求∠A的度数。
、G9,,若∠BDC=1400,∠BG1C=77°,求∠A的度数。


⑴观察“规形图”,试探究∠BDC与∠A、∠B、∠C之间的关系,并说明理由;
⑵请你直接利用以上结论,解决以下三个问题:
①如图(2),把一块三角尺XYZ放置在△ABC上,使三角尺的两条直角边XY、XZ恰好经过点B、C,若∠A=50°,则∠ABX+∠ACX =__________°;
②如图(3),DC平分∠ADB, EC平分∠AEB,若∠DAE=50°,∠DBE=130°,求∠DCE的度数;
③如图(4),∠ABD,∠ACD的10等分线相交于点G1、G2
 、G9,,若∠BDC=1400,∠BG1C=77°,求∠A的度数。
、G9,,若∠BDC=1400,∠BG1C=77°,求∠A的度数。(1)∠BDC=∠A+∠B+∠C(2)40°,∠DCE=90°,∠A为70°
试题分析:解:(1)连接AD并延长至点F,
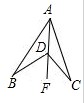
由外角定理可得∠BDF=∠BAD+∠B,∠CDF=∠C+∠CAD;且∠BDC=∠BDF+∠CDF及∠BAC=∠BAD+∠CAD;
相加可得∠BDC=∠A+∠B+∠C;
(2)①由(1)的结论易得:∠ABX+∠ACX+∠A=∠BXC,
又因为∠A=50°,∠BXC=90°,所以∠ABX+∠ACX=90°-50°=40°;
②由(1)的结论易得∠DBE=∠A+∠ADB+∠AEB,易得∠ADB+∠AEB=80°;而∠DCE=
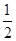
(∠ADB+∠AEB)+∠A,代入∠DAE=50°,∠DBE=130°,易得∠DCE=90°;
③∠BG1C═
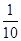 (∠ABD+∠ACD)+∠A,
(∠ABD+∠ACD)+∠A,∵∠BG1C=77°,∴设∠A为x°,∵∠ABD+∠ACD=140°-x°
∴
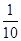 (140-x)+x=77,14-
(140-x)+x=77,14-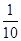 x+x=77,x=70∴∠A为70°.
x+x=77,x=70∴∠A为70°.点评:本题难度较大。需要学生用已学的知识点进行探究规律与归纳计算。在做这类题型时,通常第一二问较容易求证,而第三问要结合前面2个证明总结出规律来进行计算。

练习册系列答案
 黄冈创优卷系列答案
黄冈创优卷系列答案
相关题目
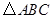 绕点
绕点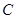 顺利针方向旋转
顺利针方向旋转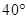 得
得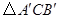 ,若
,若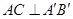 ,则
,则 等于( )
等于( )
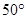 (B)
(B) (C)
(C)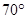 (D)
(D)
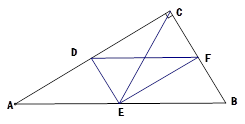

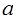 为偶数,且
为偶数,且 ,则这个三角形的周长为_______________。
,则这个三角形的周长为_______________。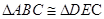 ,
,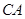 和
和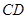 ,
,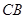 和
和 是对应边,若
是对应边,若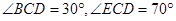 ,则
,则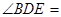 ____________
____________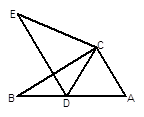
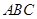 中,
中,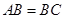 ,
,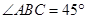 ,
,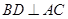 于
于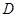 ,
,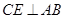 于点
于点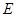 ,
, 、
、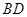 相交于
相交于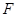 .
.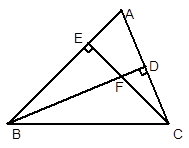
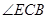 的度数;
的度数;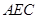 ≌△
≌△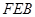 ;
;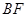 与
与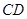 的数量关系,并给予证明.
的数量关系,并给予证明.